Refine listing
Actions for selected content:
1959 results in 20xxx
THE SYMMETRIC GROUP REPRESENTATION ON COHOMOLOGY OF THE REGULAR ELEMENTS OF A MAXIMAL TORUS OF THE SPECIAL LINEAR GROUP
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 1 / February 2008
- Published online by Cambridge University Press:
- 01 February 2008, pp. 85-98
- Print publication:
- February 2008
-
- Article
-
- You have access
- Export citation
On finite generation and presentability of Schützenberger products
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 83 / Issue 3 / December 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 357-368
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
Quasiregular self-mappings of manifolds and word hyperbolic groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 143 / Issue 6 / November 2007
- Published online by Cambridge University Press:
- 01 November 2007, pp. 1613-1622
- Print publication:
- November 2007
-
- Article
-
- You have access
- Export citation
Recognizing powers in nilpotent groups and nilpotent images of free groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 83 / Issue 2 / October 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 149-156
- Print publication:
- October 2007
-
- Article
-
- You have access
- Export citation
Large doubly transitive orbits on a line
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 83 / Issue 2 / October 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 227-270
- Print publication:
- October 2007
-
- Article
-
- You have access
- Export citation
Canonical Varieties of Completely Regular Semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 83 / Issue 1 / August 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 87-104
- Print publication:
- August 2007
-
- Article
-
- You have access
- Export citation
Rate of escape of random walks on free products
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 83 / Issue 1 / August 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 31-54
- Print publication:
- August 2007
-
- Article
-
- You have access
- Export citation
Monothetic algebraic groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 82 / Issue 3 / June 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 315-324
- Print publication:
- June 2007
-
- Article
-
- You have access
- Export citation
On the module structure of a group action on a Lie algebra
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 82 / Issue 2 / April 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 237-248
- Print publication:
- April 2007
-
- Article
-
- You have access
- Export citation
On the square root of the centre of the Hecke algebra of type A
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 82 / Issue 2 / April 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 209-220
- Print publication:
- April 2007
-
- Article
-
- You have access
- Export citation
THE SPECTRA OF THE SPHERICAL AND EUCLIDEAN TRIANGLE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 2 / April 2008
- Published online by Cambridge University Press:
- 01 April 2007, pp. 217-227
- Print publication:
- April 2008
-
- Article
-
- You have access
- Export citation
On parabolic submonoids of a class of singular Artin monoids
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 82 / Issue 1 / February 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 29-37
- Print publication:
- February 2007
-
- Article
-
- You have access
- Export citation
Inverse semigroups determined by their partial automorphism monoids
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 81 / Issue 2 / October 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 185-198
- Print publication:
- October 2006
-
- Article
-
- You have access
- Export citation
Cubic symmetric graphs of order twice an odd prime-power
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 81 / Issue 2 / October 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 153-164
- Print publication:
- October 2006
-
- Article
-
- You have access
- Export citation
The palindromic width of a free product of groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 81 / Issue 2 / October 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 199-208
- Print publication:
- October 2006
-
- Article
-
- You have access
- Export citation
Elements of minimal breadth in finite p-groups and lie algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 81 / Issue 2 / October 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 209-214
- Print publication:
- October 2006
-
- Article
-
- You have access
- Export citation
The commutator subgroup and Schur multiplier of a pair of finite p-groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 81 / Issue 1 / August 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-10
- Print publication:
- August 2006
-
- Article
-
- You have access
- Export citation
A property of the complex semigroup algebra of a free monoid
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 81 / Issue 1 / August 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 97-104
- Print publication:
- August 2006
-
- Article
-
- You have access
- Export citation
Multialgebras, universal algebras and identities
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 81 / Issue 1 / August 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 121-140
- Print publication:
- August 2006
-
- Article
-
- You have access
- Export citation
Polyhedral convex cones and the equational theory of the bicyclic semigroup
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 81 / Issue 1 / August 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 63-96
- Print publication:
- August 2006
-
- Article
-
- You have access
- Export citation
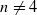 ), then every quasiregular mapping
), then every quasiregular mapping 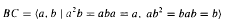 or in the semigroup
or in the semigroup 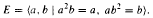 . The semigroups
. The semigroups 