Refine listing
Actions for selected content:
1959 results in 20xxx
On a family of cyclically-presented fundamental groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 2 / October 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 235-242
- Print publication:
- October 2001
-
- Article
-
- You have access
- Export citation
Young modules for symmetric groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 2 / October 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 201-210
- Print publication:
- October 2001
-
- Article
-
- You have access
- Export citation
Bounds on finite quasiprimitive permutation groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 2 / October 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 243-258
- Print publication:
- October 2001
-
- Article
-
- You have access
- Export citation
Lie powers of free modules for certain groups of prime power order
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 2 / October 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 149-158
- Print publication:
- October 2001
-
- Article
-
- You have access
- Export citation
A note on minimal coverings of groups by subgroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 2 / October 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 159-168
- Print publication:
- October 2001
-
- Article
-
- You have access
- Export citation
On (2, 3, 7)-generation of maximal parabolic subgroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 2 / October 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 187-200
- Print publication:
- October 2001
-
- Article
-
- You have access
- Export citation
Restricted Lazard elimination and modular Lie powers
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 2 / October 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 259-278
- Print publication:
- October 2001
-
- Article
-
- You have access
- Export citation
Cyclic permutable subgroups of finite groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 2 / October 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 169-176
- Print publication:
- October 2001
-
- Article
-
- You have access
- Export citation
Ensuring commutativity of finite groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 2 / October 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 233-234
- Print publication:
- October 2001
-
- Article
-
- You have access
- Export citation
Automorphisms of Cayley graphs of metacyclic groups of prime-power order
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 2 / October 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 223-232
- Print publication:
- October 2001
-
- Article
-
- You have access
- Export citation
On the probability of generating a minimal d-generated group
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 2 / October 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 177-186
- Print publication:
- October 2001
-
- Article
-
- You have access
- Export citation
Towers, ladders and the B. B. Newman Spelling Theorem
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 1 / August 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 53-69
- Print publication:
- August 2001
-
- Article
-
- You have access
- Export citation
Nilpotency indices of the radicals of finite p-solvable group algebras, I
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 1 / August 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 117-133
- Print publication:
- August 2001
-
- Article
-
- You have access
- Export citation
Semidistributive inverse semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 1 / August 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 37-51
- Print publication:
- August 2001
-
- Article
-
- You have access
- Export citation
A problem of expressibility in some amalgamated products of groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 1 / August 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 105-115
- Print publication:
- August 2001
-
- Article
-
- You have access
- Export citation
Remarks concerning finitely generated semigroups having regular sets of unique normal forms
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 70 / Issue 3 / June 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 293-310
- Print publication:
- June 2001
-
- Article
-
- You have access
- Export citation
The structure of finite groups in which permutability is a transitive relation
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 70 / Issue 2 / April 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 143-160
- Print publication:
- April 2001
-
- Article
-
- You have access
- Export citation
Locally full HNN extensions of inverse semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 70 / Issue 2 / April 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 235-272
- Print publication:
- April 2001
-
- Article
-
- You have access
- Export citation
On profinite groups in which commutators are Engel
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 70 / Issue 1 / February 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-9
- Print publication:
- February 2001
-
- Article
-
- You have access
- Export citation
On real forms of a complex algebraic curve
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 70 / Issue 1 / February 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 134-142
- Print publication:
- February 2001
-
- Article
-
- You have access
- Export citation
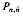 of
of 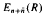 consisting of the matrices of shape
consisting of the matrices of shape 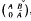 , where
, where 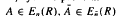 and
and 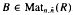 , is (2, 3, 7)-generated whenever
, is (2, 3, 7)-generated whenever 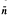 are large enough.
are large enough.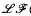 (
(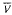 (
(