Refine listing
Actions for selected content:
1959 results in 20xxx
Some covering theorems for locally inverse semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 39 / Issue 1 / August 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 63-74
- Print publication:
- August 1985
-
- Article
-
- You have access
- Export citation
Varieties of completely regular semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 38 / Issue 3 / June 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 372-393
- Print publication:
- June 1985
-
- Article
-
- You have access
- Export citation
Nilpotent orbits of exceptional Lie algebras over algebraically closed fields of bad characteristic
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 38 / Issue 3 / June 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 330-350
- Print publication:
- June 1985
-
- Article
-
- You have access
- Export citation
Some properties of periodic modules
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 38 / Issue 3 / June 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 408-415
- Print publication:
- June 1985
-
- Article
-
- You have access
- Export citation
The structure of a group of permutation polynomials
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 38 / Issue 2 / April 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 164-170
- Print publication:
- April 1985
-
- Article
-
- You have access
- Export citation
Nil and s-prime Ω-groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 38 / Issue 2 / April 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 222-229
- Print publication:
- April 1985
-
- Article
-
- You have access
- Export citation
Some finite groups with few defining relations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 38 / Issue 2 / April 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 230-240
- Print publication:
- April 1985
-
- Article
-
- You have access
- Export citation
Quotient closed metanilpotent Fitting classes
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 38 / Issue 2 / April 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 157-163
- Print publication:
- April 1985
-
- Article
-
- You have access
- Export citation
On the lattice of congruences on an eventually regular semigroup
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 38 / Issue 2 / April 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 281-286
- Print publication:
- April 1985
-
- Article
-
- You have access
- Export citation
On saturated permutative varieties and consequences of permutation identities
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 38 / Issue 2 / April 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 186-197
- Print publication:
- April 1985
-
- Article
-
- You have access
- Export citation
Some examples of finiteness conditions in centre-by-metabelian groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 38 / Issue 2 / April 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 171-174
- Print publication:
- April 1985
-
- Article
-
- You have access
- Export citation
A Schunck class construction and a problem concerning primitive groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 38 / Issue 1 / February 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 130-137
- Print publication:
- February 1985
-
- Article
-
- You have access
- Export citation
On the lower central factors of free centre-by-metabelian groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 38 / Issue 1 / February 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 65-75
- Print publication:
- February 1985
-
- Article
-
- You have access
- Export citation
Certain homomorphisms of the lattice of varieties of completely simple semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 37 / Issue 3 / December 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 287-306
- Print publication:
- December 1984
-
- Article
-
- You have access
- Export citation
On certain varieties of groups which are central extensions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 37 / Issue 3 / December 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 366-390
- Print publication:
- December 1984
-
- Article
-
- You have access
- Export citation
Verbal varieties of inverse semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 37 / Issue 3 / December 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 337-350
- Print publication:
- December 1984
-
- Article
-
- You have access
- Export citation
Biordered sets are biordered subsets of idempotents of semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 37 / Issue 2 / October 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 258-268
- Print publication:
- October 1984
-
- Article
-
- You have access
- Export citation
Small varieties of finite semigroups and extensions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 37 / Issue 2 / October 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 269-281
- Print publication:
- October 1984
-
- Article
-
- You have access
- Export citation
A characteristic property of PSL2(7)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 36 / Issue 3 / June 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 354-356
- Print publication:
- June 1984
-
- Article
-
- You have access
- Export citation
Epimorphisms preserving perfect radicals
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 36 / Issue 3 / June 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 357-364
- Print publication:
- June 1984
-
- Article
-
- You have access
- Export citation
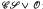 is a precisely determined subdirect product of the lattice of subvarieties of
is a precisely determined subdirect product of the lattice of subvarieties of 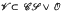 in terms of bases of identities for
in terms of bases of identities for 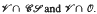 . Several operators on the lattice of subvarieties of
. Several operators on the lattice of subvarieties of 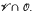 are also introduced and studied.
are also introduced and studied.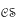 , of algebras with the operations of multiplication and inversion. It is known that the mapping
, of algebras with the operations of multiplication and inversion. It is known that the mapping 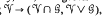 , where
, where 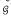 is the variety of all groups, is an isomorphism of the lattice
is the variety of all groups, is an isomorphism of the lattice 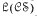 of all subvarieties of
of all subvarieties of 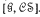 . We consider embeddings of
. We consider embeddings of 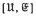 of all groups which are central extensions by groups in
of all groups which are central extensions by groups in 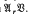 . Here
. Here 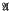 , is the variety of abelian groups of exponent dividing
, is the variety of abelian groups of exponent dividing 