Refine listing
Actions for selected content:
51 results in 19Dxx
On exact
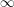 $\infty$-categories and the Theorem of the Heart
$\infty$-categories and the Theorem of the Heart
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 11 / November 2015
- Published online by Cambridge University Press:
- 19 August 2015, pp. 2160-2186
- Print publication:
- November 2015
-
- Article
- Export citation
Projective geometry in characteristic one and the epicyclic category
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 217 / March 2015
- Published online by Cambridge University Press:
- 11 January 2016, pp. 95-132
- Print publication:
- March 2015
-
- Article
-
- You have access
- Export citation
PRO CDH-DESCENT FOR CYCLIC HOMOLOGY AND
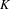 $K$-THEORY
$K$-THEORY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 3 / July 2016
- Published online by Cambridge University Press:
- 27 November 2014, pp. 539-567
- Print publication:
- July 2016
-
- Article
-
- You have access
- Export citation
Vanishing of negative
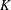 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}K$-theory in positive characteristic
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}K$-theory in positive characteristic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 8 / August 2014
- Published online by Cambridge University Press:
- 17 July 2014, pp. 1425-1434
- Print publication:
- August 2014
-
- Article
- Export citation
Noncommutative motives of Azumaya algebras
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 14 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 10 March 2014, pp. 379-403
- Print publication:
- April 2015
-
- Article
- Export citation
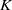 $K$ -theory of one-dimensional rings via pro-excision
$K$ -theory of one-dimensional rings via pro-excision
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 23 July 2013, pp. 225-272
- Print publication:
- April 2014
-
- Article
- Export citation
Rationality problems and conjectures of Milnor and Bloch–Kato
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 8 / August 2013
- Published online by Cambridge University Press:
- 03 June 2013, pp. 1312-1326
- Print publication:
- August 2013
-
- Article
- Export citation
Kontsevich’s noncommutative numerical motives
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 6 / November 2012
- Published online by Cambridge University Press:
- 12 October 2012, pp. 1811-1820
- Print publication:
- November 2012
-
- Article
-
- You have access
- Export citation
Non-connective K-theory via universal invariants
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 4 / July 2011
- Published online by Cambridge University Press:
- 04 May 2011, pp. 1281-1320
- Print publication:
- July 2011
-
- Article
-
- You have access
- Export citation
Hochschild cohomology of tensor products of topological algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 2 / June 2010
- Published online by Cambridge University Press:
- 30 April 2010, pp. 447-470
-
- Article
-
- You have access
- Export citation
Differential graded motives: weight complex, weight filtrations and spectral sequences for realizations; Voevodsky versus Hanamura
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 8 / Issue 1 / January 2009
- Published online by Cambridge University Press:
- 16 October 2008, pp. 39-97
- Print publication:
- January 2009
-
- Article
- Export citation
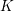
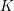
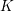
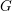
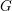
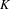
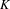
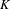
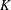
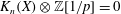
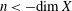
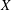
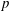
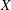
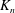
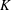
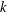
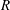
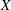
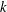
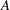
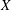

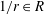
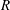
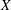
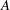
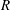
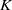
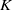
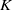
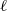
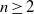

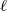
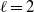
 -algebras which are Fréchet spaces or nuclear
-algebras which are Fréchet spaces or nuclear  (and give a ‘differential graded enhancement’ of it). This enables us to able to verify that DM
(and give a ‘differential graded enhancement’ of it). This enables us to able to verify that DM (
(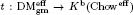 ;
; 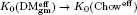 . A motif is mixed Tate whenever its weight complex is. Over finite fields the Beilinson–Parshin conjecture holds if and only if
. A motif is mixed Tate whenever its weight complex is. Over finite fields the Beilinson–Parshin conjecture holds if and only if 