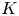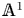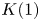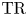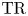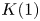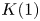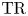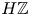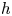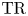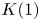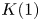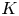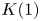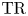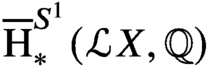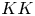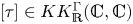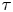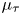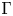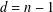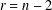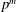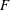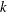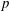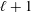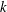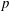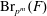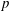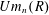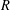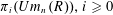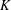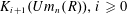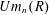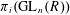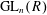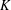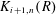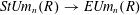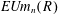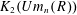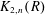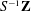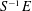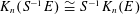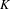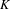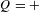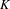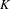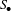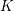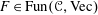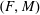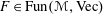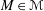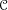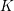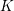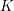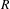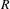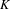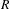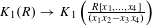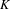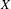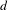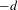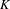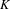Refine listing
Actions for selected content:
53 results in 19Dxx
K-theory of valuation rings
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 6 / June 2021
- Published online by Cambridge University Press:
- 20 May 2021, pp. 1121-1142
- Print publication:
- June 2021
-
- Article
- Export citation
Towards Vorst's conjecture in positive characteristic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 6 / June 2021
- Published online by Cambridge University Press:
- 20 May 2021, pp. 1143-1171
- Print publication:
- June 2021
-
- Article
- Export citation
On
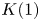 $K(1)$-local
$K(1)$-local 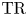 $\mathrm {TR}$
$\mathrm {TR}$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 04 May 2021, pp. 1079-1119
- Print publication:
- May 2021
-
- Article
- Export citation
Hodge decomposition of string topology
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 13 April 2021, e33
-
- Article
-
- You have access
- Open access
- Export citation
Twisted Donaldson invariants
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 3 / November 2021
- Published online by Cambridge University Press:
- 04 February 2021, pp. 515-568
- Print publication:
- November 2021
-
- Article
- Export citation
The symplectic geometry of higher Auslander algebras: Symmetric products of disks
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 01 February 2021, e10
-
- Article
-
- You have access
- Open access
- Export citation
The categorified Grothendieck–Riemann–Roch theorem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 15 February 2021, pp. 154-214
- Print publication:
- January 2021
-
- Article
- Export citation
The Baum–Connes conjecture localised at the unit element of a discrete group
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 14 January 2021, pp. 2536-2559
- Print publication:
- December 2020
-
- Article
- Export citation
TOPOLOGIES ON SCHEMES AND MODULUS PAIRS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 244 / December 2021
- Published online by Cambridge University Press:
- 13 July 2020, pp. 283-313
- Print publication:
- December 2021
-
- Article
- Export citation
RIGIDIFIED TORSOR COCYCLES, HYPERCOVERINGS AND BUNDLE GERBES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 07 April 2020, pp. 115-144
- Print publication:
- February 2022
-
- Article
- Export citation
Essential Dimension, Symbol Length and
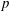 $p$-rank
$p$-rank
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 04 February 2020, pp. 882-890
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
GLOBAL ACTIONS AND VECTOR
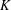 $K$-THEORY
$K$-THEORY
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 15 January 2020, e4
-
- Article
-
- You have access
- Open access
- Export citation
CATEGORIFYING RATIONALIZATION
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 09 January 2020, e42
-
- Article
-
- You have access
- Open access
- Export citation
HIGHER
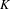 $K$-THEORY OF FORMS I. FROM RINGS TO EXACT CATEGORIES
$K$-THEORY OF FORMS I. FROM RINGS TO EXACT CATEGORIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 4 / July 2021
- Published online by Cambridge University Press:
- 02 August 2019, pp. 1205-1273
- Print publication:
- July 2021
-
- Article
- Export citation
CHERN CLASSES WITH MODULUS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 236 / December 2019
- Published online by Cambridge University Press:
- 01 February 2019, pp. 84-133
- Print publication:
- December 2019
-
- Article
-
- You have access
- HTML
- Export citation
Monoidal Categories, 2-Traces, and Cyclic Cohomology
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 293-312
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
Excision in algebraic
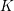 $K$-theory revisited
$K$-theory revisited
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 9 / September 2018
- Published online by Cambridge University Press:
- 06 August 2018, pp. 1801-1814
- Print publication:
- September 2018
-
- Article
- Export citation
GENERALIZED THOM SPECTRA AND THEIR TOPOLOGICAL HOCHSCHILD HOMOLOGY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 02 November 2017, pp. 21-64
- Print publication:
- January 2020
-
- Article
- Export citation
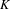 $K$-THEORY OF MONOID ALGEBRAS AND A QUESTIONOF GUBELADZE
$K$-THEORY OF MONOID ALGEBRAS AND A QUESTIONOF GUBELADZE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 5 / September 2019
- Published online by Cambridge University Press:
- 10 August 2017, pp. 1051-1085
- Print publication:
- September 2019
-
- Article
- Export citation
VANISHING OF THE NEGATIVE HOMOTOPY
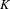 $K$-THEORY OF QUOTIENT SINGULARITIES
$K$-THEORY OF QUOTIENT SINGULARITIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 3 / May 2019
- Published online by Cambridge University Press:
- 08 May 2017, pp. 619-627
- Print publication:
- May 2019
-
- Article
- Export citation