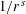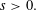Refine listing
Actions for selected content:
48 results in 11Cxx
INVERSE BERNSTEIN INEQUALITIES AND MIN–MAX–MIN PROBLEMS ON THE UNIT CIRCLE
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 13 August 2014, pp. 581-590
- Print publication:
- September 2015
-
- Article
- Export citation
CAUCHY–MIRIMANOFF AND RELATED POLYNOMIALS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 27 September 2012, pp. 269-280
- Print publication:
- April 2012
-
- Article
-
- You have access
- Export citation
Proof of the Hamiltonicity-Trace Conjecture for Singularly Perturbed Markov Chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 4 / December 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 901-910
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation
ON THE DISTRIBUTION OF GALOIS GROUPS
- Part of
-
- Journal:
- Mathematika / Volume 58 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 21 October 2011, pp. 35-44
- Print publication:
- January 2012
-
- Article
- Export citation
Bounds for the multiplicities of the roots of a complex polynomial
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 3 / October 2011
- Published online by Cambridge University Press:
- 08 April 2011, pp. 587-598
-
- Article
-
- You have access
- Export citation
THE TRACE PROBLEM FOR TOTALLY POSITIVE ALGEBRAIC INTEGERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 90 / Issue 3 / June 2011
- Published online by Cambridge University Press:
- 17 February 2011, pp. 341-354
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
Moyennes de certaines fonctions multiplicatives sur les entiers friables, 3
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 2 / March 2008
- Published online by Cambridge University Press:
- 01 March 2008, pp. 339-376
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
On Integer Polynomials with Multiple Roots
- Part of
-
- Journal:
- Mathematika / Volume 54 / Issue 1-2 / December 2007
- Published online by Cambridge University Press:
- 21 December 2009, pp. 83-92
- Print publication:
- December 2007
-
- Article
- Export citation