Refine listing
Actions for selected content:
48 results in 11Cxx
ON THE DIVISIBILITY AMONG POWER LCM MATRICES ON GCD-CLOSED SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 19 May 2022, pp. 31-39
- Print publication:
- February 2023
-
- Article
- Export citation
Combinatorial and harmonic-analytic methods for integer tilings
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 09 March 2022, e8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On monic abelian cubics
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 16 May 2022, pp. 550-567
- Print publication:
- March 2022
-
- Article
- Export citation
APPLICATIONS OF CIRCULANT MATRICES TO DETERMINANTS INVOLVING
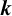 $\boldsymbol {k}$TH POWER RESIDUES
$\boldsymbol {k}$TH POWER RESIDUES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 09 February 2022, pp. 243-253
- Print publication:
- October 2022
-
- Article
- Export citation
AN EFFECTIVE ANALYTIC FORMULA FOR THE NUMBER OF DISTINCT IRREDUCIBLE FACTORS OF A POLYNOMIAL
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 09 December 2021, pp. 339-356
- Print publication:
- December 2022
-
- Article
- Export citation
A NOTE ON GIRSTMAIR’S IRREDUCIBILITY CRITERION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 04 November 2021, pp. 62-66
- Print publication:
- August 2022
-
- Article
- Export citation
HANKEL DETERMINANTS OF FACTORIAL FRACTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 07 June 2021, pp. 46-57
- Print publication:
- February 2022
-
- Article
- Export citation
Volume function and Mahler measure of exact polynomials
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 4 / April 2021
- Published online by Cambridge University Press:
- 14 April 2021, pp. 809-834
- Print publication:
- April 2021
-
- Article
- Export citation
On intersections of polynomial semigroups orbits with plane lines
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 17 July 2020, pp. 442-451
- Print publication:
- June 2021
-
- Article
- Export citation
Large values of Dirichlet L-functions at zeros of a class of L-functions
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 01 July 2020, pp. 1459-1505
- Print publication:
- December 2021
-
- Article
- Export citation
SUM-PRODUCT ESTIMATES FOR DIAGONAL MATRICES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 24 June 2020, pp. 28-37
- Print publication:
- February 2021
-
- Article
- Export citation
Determinantal inequalities for the partition function
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 29 January 2019, pp. 1451-1466
- Print publication:
- June 2020
-
- Article
- Export citation
A CLASS OF IRREDUCIBLE POLYNOMIALS ASSOCIATED WITH PRIME DIVISORS OF VALUES OF CYCLOTOMIC POLYNOMIALS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 4 / 2019
- Published online by Cambridge University Press:
- 14 August 2019, pp. 1033-1037
- Print publication:
- 2019
-
- Article
- Export citation
NOTE ON THE NUMBER OF DIVISORS OF REDUCIBLE QUADRATIC POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 15 August 2018, pp. 1-9
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
CONTINUITY OF ROOTS, REVISITED
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 15 August 2018, pp. 448-455
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
MORE ON A CERTAIN ARITHMETICAL DETERMINANT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 17 October 2017, pp. 15-25
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
ON POLYNOMIALS WHOSE ROOTS HAVE RATIONAL QUOTIENT OF DIFFERENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 05 July 2017, pp. 185-190
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
ITERATION OF QUADRATIC POLYNOMIALS OVER FINITE FIELDS
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 1041-1059
- Print publication:
- 2017
-
- Article
- Export citation
TOPICS IN DIVISIBILITY: PAIRWISE COPRIMALITY, THE GCD OF SHIFTED SETS AND POLYNOMIAL IRREDUCIBILITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 02 January 2016, pp. 167-168
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
On a generalization of a waiting time problem and some combinatorial identities
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 30 March 2016, pp. 981-989
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
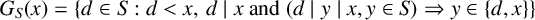
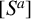

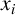
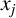
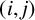
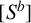
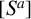
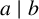
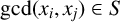
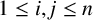
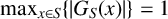

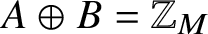
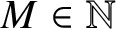
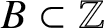
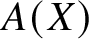
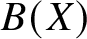
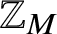
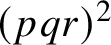
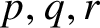
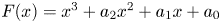
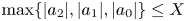
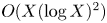
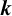


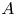
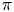
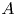
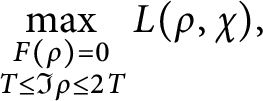
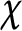
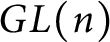
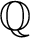
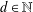
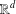
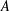
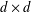
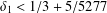
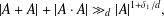
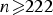
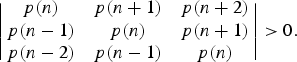

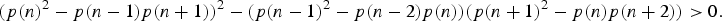

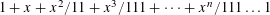
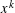
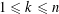
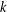
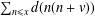

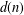

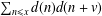
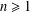
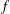
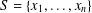

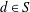
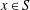
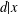
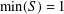
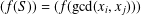
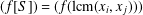
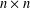
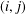
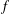
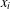
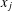
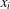
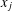
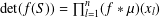
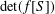
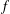
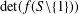
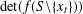

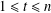
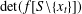
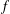
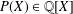
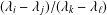
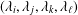
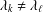
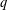
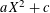
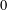
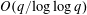
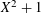
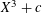
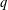
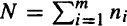 Let
Let 