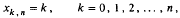Refine listing
Actions for selected content:
75 results in 65Dxx
QUASI-MONTE CARLO METHODS FOR HIGH-DIMENSIONAL INTEGRATION: THE STANDARD (WEIGHTED HILBERT SPACE) SETTING AND BEYOND
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 53 / Issue 1 / July 2011
- Published online by Cambridge University Press:
- 29 May 2012, pp. 1-37
-
- Article
-
- You have access
- Export citation
GENERAL THREE-POINT QUADRATURE FORMULAS OF EULER TYPE
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 52 / Issue 3 / January 2011
- Published online by Cambridge University Press:
- 05 December 2011, pp. 309-317
-
- Article
-
- You have access
- Export citation
AN INTEGRAL EQUATION FOR THE DISTRIBUTION OF THE FIRST EXIT TIME OF A REFLECTED BROWNIAN MOTION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 4 / April 2009
- Published online by Cambridge University Press:
- 04 December 2009, pp. 445-454
-
- Article
-
- You have access
- Export citation
THE BEST LEAST ABSOLUTE DEVIATIONS LINE – PROPERTIES AND TWO EFFICIENT METHODS FOR ITS DERIVATION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 2 / October 2008
- Published online by Cambridge University Press:
- 01 October 2008, pp. 185-198
-
- Article
-
- You have access
- Export citation
LOCAL RADIAL BASIS FUNCTION APPROXIMATION ON THE SPHERE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 2 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 197-224
- Print publication:
- April 2008
-
- Article
-
- You have access
- Export citation
QUINTIC B-SPLINE COLLOCATION METHOD FOR NUMERICAL SOLUTION OF THE RLW EQUATION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 49 / Issue 3 / January 2008
- Published online by Cambridge University Press:
- 01 January 2008, pp. 389-410
-
- Article
-
- You have access
- Export citation
Transforming a random variable to a prescribed distribution: an application to school-based assessment
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue A / 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 239-252
- Print publication:
- 2004
-
- Article
- Export citation
On the correlation structure of unilateral AR processes on the plane
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 2 / June 2000
- Published online by Cambridge University Press:
- 01 July 2016, pp. 408-425
- Print publication:
- June 2000
-
- Article
- Export citation
Approximations of boundary crossing probabilities for a Brownian motion
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 4 / December 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1019-1030
- Print publication:
- December 1999
-
- Article
- Export citation
Estimating Functionals of a Stochastic Process
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 29 / Issue 1 / March 1997
- Published online by Cambridge University Press:
- 01 July 2016, pp. 249-270
- Print publication:
- March 1997
-
- Article
- Export citation
Equivalent necessary and sufficient conditions on noise sequences for stochastic approximation algorithms
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 784-801
- Print publication:
- September 1996
-
- Article
- Export citation
Stereological estimation of particle size distributions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 27 / Issue 2 / June 1995
- Published online by Cambridge University Press:
- 01 July 2016, pp. 350-366
- Print publication:
- June 1995
-
- Article
- Export citation
Convergence of the backfitting algorithm for additive models
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 57 / Issue 3 / December 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 316-329
- Print publication:
- December 1994
-
- Article
-
- You have access
- Export citation
On the Lebesgue function for lagrange interpolation with equidistant nodes
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 52 / Issue 1 / February 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 111-118
- Print publication:
- February 1992
-
- Article
-
- You have access
- Export citation
On an inversion theorem of Möbius
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 30 / Issue 1 / September 1980
- Published online by Cambridge University Press:
- 09 April 2009, pp. 15-32
- Print publication:
- September 1980
-
- Article
-
- You have access
- Export citation
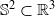 . More precisely, we consider radial basis function interpolation based on data on a (global or local) point set
. More precisely, we consider radial basis function interpolation based on data on a (global or local) point set 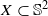 for functions in the Sobolev space
for functions in the Sobolev space 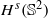 with norm
with norm 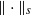 , where
, where 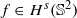 satisfies
satisfies 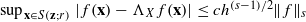 , where
, where