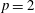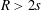Refine listing
Actions for selected content:
58 results in 65Lxx
Perturbation Bounds and Condition Numbers for a Complex Indefinite Linear Algebraic System
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 6 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 12 May 2016, pp. 211-221
- Print publication:
- May 2016
-
- Article
- Export citation
Multilevel Circulant Preconditioner for High-Dimensional Fractional Diffusion Equations
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 6 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 12 May 2016, pp. 109-130
- Print publication:
- May 2016
-
- Article
- Export citation
A Multigrid Method for Ground State Solution of Bose-Einstein Condensates
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 3 / March 2016
- Published online by Cambridge University Press:
- 16 March 2016, pp. 648-662
- Print publication:
- March 2016
-
- Article
- Export citation
A computational iterative method for solving nonlinear ordinary differential equations
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 December 2015, pp. 730-753
-
- Article
-
- You have access
- Export citation
An L∞-error Estimate for theh-p Version Continuous Petrov-Galerkin Method for NonlinearInitial Value Problems
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 5 / Issue 4 / November 2015
- Published online by Cambridge University Press:
- 10 November 2015, pp. 301-311
- Print publication:
- November 2015
-
- Article
- Export citation
Superoptimal Preconditioners for Functions of Matrices
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 8 / Issue 4 / November 2015
- Published online by Cambridge University Press:
- 10 November 2015, pp. 515-529
- Print publication:
- November 2015
-
- Article
- Export citation
Backward Error Analysis for Eigenproblems Involving Conjugate Symplectic Matrices
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 5 / Issue 4 / November 2015
- Published online by Cambridge University Press:
- 10 November 2015, pp. 312-326
- Print publication:
- November 2015
-
- Article
- Export citation
A Multilevel Correction Method for Steklov Eigenvalue Problem by Nonconforming Finite Element Methods
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 8 / Issue 3 / August 2015
- Published online by Cambridge University Press:
- 05 August 2015, pp. 383-405
- Print publication:
- August 2015
-
- Article
- Export citation
The Runge–Kutta method in geometric multiplicative calculus
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 August 2015, pp. 539-554
-
- Article
-
- You have access
- Export citation
Long Time Behaviour of an Exponential Integrator for a Vlasov-Poisson System with Strong Magnetic Field
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 18 / Issue 2 / August 2015
- Published online by Cambridge University Press:
- 30 July 2015, pp. 263-296
- Print publication:
- August 2015
-
- Article
- Export citation
LARGE INTERVAL SOLUTION OF THE EMDEN–FOWLER EQUATION USING A MODIFIED ADOMIAN DECOMPOSITION METHOD WITH AN INTEGRATING FACTOR
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 56 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 15 December 2014, pp. 192-208
-
- Article
-
- You have access
- Export citation
Rational functions with maximal radius of absolute monotonicity
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 May 2014, pp. 159-205
-
- Article
-
- You have access
- Export citation
AN ADOMIAN DECOMPOSITION METHOD FOR SOLVING LIÉNARD EQUATIONS IN GENERAL FORM
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 51 / Issue 2 / October 2009
- Published online by Cambridge University Press:
- 05 March 2010, pp. 302-308
-
- Article
-
- You have access
- Export citation
Eigenvalue enclosures and exclosures for non-self-adjoint problems in hydrodynamics
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 01 March 2010, pp. 65-81
-
- Article
-
- You have access
- Export citation
PRACTICAL RUNGE–KUTTA METHODS FOR SCIENTIFIC COMPUTATION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 3 / January 2009
- Published online by Cambridge University Press:
- 03 November 2009, pp. 333-342
-
- Article
-
- You have access
- Export citation
RECONSIDERING TRIGONOMETRIC INTEGRATORS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 3 / January 2009
- Published online by Cambridge University Press:
- 03 November 2009, pp. 320-332
-
- Article
-
- You have access
- Export citation
Archimedean copulas, exchangeability, and max-stability
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 383-390
- Print publication:
- June 1994
-
- Article
- Export citation
Uniform convergence of regularization methods for Fredholm equations of the first kind
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 39 / Issue 2 / October 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 282-286
- Print publication:
- October 1985
-
- Article
-
- You have access
- Export citation