Refine listing
Actions for selected content:
58 results in 65Lxx
Detached Eddy Simulation of Complex Separation Flows Over a Modern Fighter Model at High Angle of Attack
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 22 / Issue 5 / November 2017
- Published online by Cambridge University Press:
- 31 October 2017, pp. 1309-1332
- Print publication:
- November 2017
-
- Article
- Export citation
A NEW MINIMIZATION PRINCIPLE FOR THE POISSON EQUATION LEADING TO A FLEXIBLE FINITE ELEMENT APPROACH
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 59 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 03 October 2017, pp. 232-239
-
- Article
-
- You have access
- Export citation
Computable Error Estimates for a Nonsymmetric Eigenvalue Problem
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 7 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 07 September 2017, pp. 583-602
- Print publication:
- August 2017
-
- Article
- Export citation
A High-Order Method for Weakly Compressible Flows
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 22 / Issue 4 / October 2017
- Published online by Cambridge University Press:
- 28 July 2017, pp. 1150-1174
- Print publication:
- October 2017
-
- Article
- Export citation
An Essential Extension of the Finite-Energy Condition for Extended Runge-Kutta-Nyström Integrators when Applied to Nonlinear Wave Equations
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 22 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 06 July 2017, pp. 742-764
- Print publication:
- September 2017
-
- Article
- Export citation
A Domain Decomposition Based Spectral Collocation Method for Lane-Emden Equations
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 22 / Issue 2 / August 2017
- Published online by Cambridge University Press:
- 21 June 2017, pp. 542-571
- Print publication:
- August 2017
-
- Article
- Export citation
A Hybrid Spectral Element Method for Fractional Two-Point Boundary Value Problems
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 10 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 09 May 2017, pp. 437-464
- Print publication:
- May 2017
-
- Article
- Export citation
Application of gPCRK Methods to Nonlinear Random Differential Equations with Piecewise Constant Argument
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 7 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 02 May 2017, pp. 306-324
- Print publication:
- May 2017
-
- Article
- Export citation
Exponential Additive Runge-Kutta Methods for Semi-Linear Differential Equations
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 7 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 02 May 2017, pp. 286-305
- Print publication:
- May 2017
-
- Article
- Export citation
A Stochastic Galerkin Method for the Boltzmann Equation with Multi-Dimensional Random Inputs Using Sparse Wavelet Bases
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 10 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 09 May 2017, pp. 465-488
- Print publication:
- May 2017
-
- Article
- Export citation
An Explicit Hermite-Taylor Method for the Schrödinger Equation
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 21 / Issue 5 / May 2017
- Published online by Cambridge University Press:
- 27 March 2017, pp. 1207-1230
- Print publication:
- May 2017
-
- Article
- Export citation
Adapted Nested Force-Gradient Integrators: The Schwinger Model Case
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 21 / Issue 4 / April 2017
- Published online by Cambridge University Press:
- 08 March 2017, pp. 1141-1153
- Print publication:
- April 2017
-
- Article
- Export citation
Modification and Numerical Method for the Jiles-Atherton Hysteresis Model
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 21 / Issue 3 / March 2017
- Published online by Cambridge University Press:
- 07 February 2017, pp. 763-781
- Print publication:
- March 2017
-
- Article
- Export citation
Solving Vlasov-Poisson-Fokker-Planck Equations using NRxx method
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 21 / Issue 3 / March 2017
- Published online by Cambridge University Press:
- 07 February 2017, pp. 782-807
- Print publication:
- March 2017
-
- Article
- Export citation
Optimal Superconvergence of Energy Conserving Local Discontinuous Galerkin Methods for Wave Equations
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 21 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 05 December 2016, pp. 211-236
- Print publication:
- January 2017
-
- Article
- Export citation
A Multiple Interval Chebyshev-Gauss-Lobatto Collocation Method for Ordinary Differential Equations
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 9 / Issue 4 / November 2016
- Published online by Cambridge University Press:
- 17 November 2016, pp. 619-639
- Print publication:
- November 2016
-
- Article
- Export citation
An Adaptive Grid Method for Singularly Perturbed Time-Dependent Convection-Diffusion Problems
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 20 / Issue 5 / November 2016
- Published online by Cambridge University Press:
- 02 November 2016, pp. 1340-1358
- Print publication:
- November 2016
-
- Article
- Export citation
A Fully Discrete Spectral Method for Fisher’s Equation on the Whole Line
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 6 / Issue 4 / November 2016
- Published online by Cambridge University Press:
- 19 October 2016, pp. 400-415
- Print publication:
- November 2016
-
- Article
- Export citation
An Improved Second-Order Finite-Volume Algorithm for Detached-Eddy Simulation Based on Hybrid Grids
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 20 / Issue 2 / August 2016
- Published online by Cambridge University Press:
- 21 July 2016, pp. 459-485
- Print publication:
- August 2016
-
- Article
- Export citation
Sinc Collocation Solutions for the Integral Algebraic Equation of Index-1
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 8 / Issue 5 / October 2016
- Published online by Cambridge University Press:
- 08 July 2016, pp. 757-771
- Print publication:
- October 2016
-
- Article
- Export citation
 , where
, where 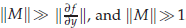 . The highly oscillatory system is due to the semi-discretisation of conservative, or dissipative, nonlinear wave equations. The structure of such a matrix
. The highly oscillatory system is due to the semi-discretisation of conservative, or dissipative, nonlinear wave equations. The structure of such a matrix 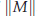 . Since stepsizes are not restricted by frequencies of
. Since stepsizes are not restricted by frequencies of 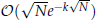 . Moreover, Sinc method is applied to several examples to illustrate the accuracy and implementation of the method.
. Moreover, Sinc method is applied to several examples to illustrate the accuracy and implementation of the method.