Refine listing
Actions for selected content:
345 results in 22Exx
Primitive ideals with bounded approximate units in L1-algebras of exponential lie groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 41 / Issue 3 / December 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 411-420
- Print publication:
- December 1986
-
- Article
-
- You have access
- Export citation
Bilinear forms and 2-dimensional cohomology
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 41 / Issue 2 / October 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 165-179
- Print publication:
- October 1986
-
- Article
-
- You have access
- Export citation
Projective representations of the infinite orthogonal group
- Part of
-
- Journal:
- Mathematika / Volume 24 / Issue 1 / June 1977
- Published online by Cambridge University Press:
- 26 February 2010, pp. 115-121
- Print publication:
- June 1977
-
- Article
- Export citation
Note on a theorem of Weil-Abels
- Part of
-
- Journal:
- Mathematika / Volume 18 / Issue 2 / December 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 185-187
- Print publication:
- December 1971
-
- Article
- Export citation
Some embeddings of Lie groups in Euclidean space
- Part of
-
- Journal:
- Mathematika / Volume 18 / Issue 1 / June 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 152-156
- Print publication:
- June 1971
-
- Article
- Export citation
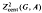 for certain 2-step nilpotent Lie groups
for certain 2-step nilpotent Lie groups 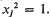
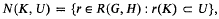
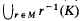 is a relatively compact subset of
is a relatively compact subset of 