We develop the Springer theory of Weyl group representations in the language of symplectic topology. Given a semisimple complex group G, we describe a Lagrangian brane in the cotangent bundle of the adjoint quotient 𝔤/G that produces the perverse sheaves of Springer theory. The main technical tool is an analysis of the Fourier transform for constructible sheaves from the perspective of the Fukaya category. Our results can be viewed as a toy model of the quantization of Hitchin fibers in the geometric Langlands program.

If G is a semisimple Lie group of real rank at least two and Γ is an irreducible lattice in G, then every homomorphism from Γ to the outer automorphism group of a finitely generated free group has finite image.

In this article a general framework for studying analytic representations of a real Lie group G is introduced. Fundamental topological properties of the representations are analyzed. A notion of temperedness for analytic representations is introduced, which indicates the existence of an action of a certain natural algebra 𝒜(G) of analytic functions of rapid decay. For reductive groups every Harish-Chandra module V is shown to admit a unique tempered analytic globalization, which is generated by V and 𝒜(G) and which embeds as the space of analytic vectors in all Banach globalizations of V.

Poincaré's Polyhedron Theorem is a widely known valuable tool in constructing manifolds endowed with a prescribed geometric structure. It is one of the few criteria providing discreteness of groups of isometries. This work contains a version of Poincaré's Polyhedron Theorem that is applicable to constructing fibre bundles over surfaces and also suits geometries of non-constant curvature. Most conditions of the theorem, being as local as possible, are easy to verify in practice.

Let M=G/K be a generalized flag manifold, that is, an adjoint orbit of a compact, connected and semisimple Lie group G. We use a variational approach to find non-Kähler homogeneous Einstein metrics for flag manifolds with two isotropy summands. We also determine the nature of these Einstein metrics as critical points of the scalar curvature functional under fixed volume.

Let G be a complex connected reductive group. The Parthasarathy–Ranga Rao–Varadarajan (PRV) conjecture, which was proved independently by S. Kumar and O. Mathieu in 1989, gives explicit irreducible submodules of the tensor product of two irreducible G-modules. This paper has three aims. First, we simplify the proof of the PRV conjecture, then we generalize it to other branching problems. Finally, we find other irreducible components of the tensor product of two irreducible G-modules that appear for ‘the same reason’ as the PRV ones.

The local Langlands conjectures imply that to every generic supercuspidal irreducible representation of G2 over a p-adic field, one can associate a generic supercuspidal irreducible representation of either PGSp6 or PGL3. We prove this conjectural dichotomy, demonstrating a precise correspondence between certain representations of G2 and other representations of PGSp6 and PGL3. This correspondence arises from theta correspondences in E6 and E7, analysis of Shalika functionals, and spin L-functions. Our main result reduces the conjectural Langlands parameterization of generic supercuspidal irreducible representations of G2 to a single conjecture about the parameterization for PGSp 6.

We set up a formalism of endoscopy for metaplectic groups. By defining a suitable transfer factor, we prove an analogue of the Langlands–Shelstad transfer conjecture for orbital integrals over any local field of characteristic zero, as well as the fundamental lemma for units of the Hecke algebra in the unramified case. This generalizes prior work of Adams and Renard in the real case and serves as a first step in studying the Arthur–Selberg trace formula for metaplectic groups.

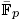Soit p un nombre premier et F un corps local non archimédien de caractéristique p. Dans cet article, à une représentation lisse irréductible de GL2(F) sur avec caractère central, nous associons un diagramme qui détermine la représentation de départ à isomorphisme près. Nous le déterminons également dans certains cas.

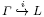Let be a lattice in the real simple Lie group 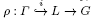L. If L is of rank at least 2 (respectively locally isomorphic to Sp(n, 1)) any unbounded morphism ρ : Γ → G into a simple real Lie group G essentially extends to a Lie morphism ρL : L → G (Margulis's superrigidity theorem, respectively Corlette's theorem). In particular any such morphism is infinitesimally, thus locally, rigid. On the other hand, for L = SU(n, 1) even morphisms of the form are not infinitesimally rigid in general. Almost nothing is known about their local rigidity. In this paper we prove that any cocompact lattice Γ in SU(n, 1) is essentially locally rigid (while in general not infinitesimally rigid) in the quaternionic groups Sp(n, 1), SU(2n, 2) or SO(4n, 4) (for the natural sequence of embeddings SU(n, 1) ⊂ Sp(n, 1) ⊂ SU(2n, 2) ⊂ SO(4n, 4)).

Suppose that G is a connected reductive group over a p-adic field F, that K is a hyperspecial maximal compact subgroup of G(F), and that V is an irreducible representation of K over the algebraic closure of the residue field of F. We establish an analogue of the Satake isomorphism for the Hecke algebra of compactly supported,K-biequivariant functions f:G(F)→End   V. These Hecke algebras were first considered by Barthel and Livné for GL 2. They play a role in the recent mod p andp-adic Langlands correspondences for GL 2 (ℚp) , in generalisations of Serre’s conjecture on the modularity of mod p Galois representations, and in the classification of irreducible mod p representations of unramified p-adic reductive groups.

Lazard showed in his seminal work (Groupes analytiques p-adiques, Publ. Math. Inst. Hautes Études Sci. 26 (1965), 389–603) that for rational coefficients, continuous group cohomology of p-adic Lie groups is isomorphic to Lie algebra cohomology. We refine this result in two directions: first, we extend Lazard’s isomorphism to integral coefficients under certain conditions; and second, we show that for algebraic groups over finite extensions K/ℚp, his isomorphism can be generalized to K-analytic cochains andK-Lie algebra cohomology.

In a paper by Badulescu [Global Jacquet–Langlands correspondence, multiplicity one and classification of automorphic representations, Invent. Math. 172 (2008), 383–438], results on the global Jacquet–Langlands correspondence, (weak and strong) multiplicity-one theorems and the classification of automorphic representations for inner forms of the general linear group over a number field were established, under the assumption that the local inner forms are split at archimedean places. In this paper, we extend the main local results of that article to archimedean places so that the above condition can be removed. Along the way, we collect several results about the unitary dual of general linear groups over ℝ, ℂ or ℍ which are of independent interest.

This work is the geometric part of our proof of the weighted fundamental lemma, which is an extension of Ngô Bao Châu’s proof of the Langlands–Shelstad fundamental lemma. Ngô’s approach is based on a study of the elliptic part of the Hichin fibration. The total space of this fibration is the algebraic stack of Hitchin bundles and its base space is the affine space of ‘characteristic polynomials’. Over the elliptic set, the Hitchin fibration is proper and the number of points of its fibers over a finite field can be expressed in terms of orbital integrals. In this paper, we study the Hitchin fibration over an open set larger than the elliptic set, namely the ‘generically regular semi-simple set’. The fibers are in general neither of finite type nor separated. By analogy with Arthur’s truncation, we introduce the substack of ξ-stable Hitchin bundles. We show that it is a Deligne–Mumford stack, smooth over the base field and proper over the base space of ‘characteristic polynomials’. Moreover, the number of points of the ξ-stable fibers over a finite field can be expressed as a sum of weighted orbital integrals, which appear in the Arthur–Selberg traceformula.

Let V be a vector space over a p-adic field F, of finite dimension, let q be a non-degenerate quadratic form over V and let D be a non-isotropic line in V. Denote by W the hyperplane orthogonal to D, and by G and H the special orthogonal groups of V and W. Let π, respectively σ, be an irreducible admissible representation of G(F) , respectively H(F) . The representation σ appears as a quotient of the restriction of π to H(F)with a certain multiplicity m(π,σ) . We know that m(π,σ)≤1 . We assume that π is supercuspidal. Then we prove a formula that computes m(π,σ)as an integral of functions deduced from the characters of π and σ. Let Π, respectively Σ, be an L-packet of tempered irreducible representations of G(F) , respectively H(F) . Here we use the sophisticated notion of L-packet due to Vogan and we assume some usual conjectural properties of those packets. A weak form of the local Gross–Prasad conjecture says that there exists a unique pair (π,σ)∈Π×Σ such that m(π,σ)=1 . Assuming that the elements of Π are supercuspidal, we prove this assertion.

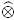We describe explicitly the continuous Hochschild and cyclic cohomology groups of certain tensor products of -algebras which are Fréchet spaces or nuclear DF-spaces. To this end we establish the existence of topological isomorphisms in the Künneth formula for the cohomology of complete nuclear DF-complexes and in the Künneth formula for continuous Hochschild cohomology of nuclear -algebras which are Fréchet spaces or DF-spaces for which all boundary maps of the standard homology complexes have closed ranges.

We show that the residue at s=0 of the standard intertwining operator attached to a supercuspidal representation π⊗χ of the Levi subgroup GL2(F)×E1 of the quasisplit group SO*6(F) defined by a quadratic extension E/F of p-adic fields is proportional to the pairing of the characters of these representations considered on the graph of the norm map of Kottwitz–Shelstad. Here π is self-dual, and the norm is simply that of Hilbert’s theorem 90. The pairing can be carried over to a pairing between the character on E1 and the character on E× defining the representation of GL2(F) when the central character of the representation is quadratic, but non-trivial, through the character identities of Labesse–Langlands. If the quadratic extension defining the representation on GL2(F) is different from E the residue is then zero. On the other hand when the central character is trivial the residue is never zero. The results agree completely with the theory of twisted endoscopy and L-functions and determines fully the reducibility of corresponding induced representations for all s.

Let k be an algebraically closed field and O = k[[t]] ⊂ F = k((t)). For an almost simple algebraic group G we classify central extensions 1 → m → E → G(F) → 1; any such extension splits canonically over G(O). Fix a positive integer N and a primitive character ζ : μN(K) → (under some assumption on the characteristic of k). Consider the category of G(O)-bi-invariant perverse sheaves on E with m-monodromy ζ. We show that this is a tensor category, which is tensor equivalent to the category of representations of a reductive group ǦE,N. We compute the root datum of ǦE,N.

Igusa varieties are smooth varieties in positive characteristic p which are closely related to Shimura varieties and Rapoport–Zink spaces. One motivation for studying Igusa varieties is to analyse the representations in the cohomology of Shimura varieties which may be ramified at p. The main purpose of this work is to stabilize the trace formula for the cohomology of Igusa varieties arising from a PEL datum of type (A) or (C). Our proof is unconditional thanks to the recent proof of the fundamental lemma by Ngô, Waldspurger and many others.

An earlier work of Kottwitz, which inspired our work and proves the stable trace formula for the special fibres of PEL Shimura varieties with good reduction, provides an explicit way to stabilize terms at ∞. Stabilization away from p and ∞ is carried out by the usual Langlands–Shelstad transfer as in work of Kottwitz. The key point of our work is to develop an explicit method to handle the orbital integrals at p. Our approach has the technical advantage that we do not need to deal with twisted orbital integrals or the twisted fundamental lemma.

One application of our formula, among others, is the computation of the arithmetic cohomology of some compact PEL-type Shimura varieties of type (A) with non-trivial endoscopy. This is worked out in a preprint of the author's entitled ‘Galois representations arising from some compact Shimura varieties’.

Let G be a reductive p-adic group. Given a compact-mod-center maximal torus S⊂G and sufficiently regular character χ of S, one can define, following Adler, Yu and others, a supercuspidal representation π(S,χ) of G. For S unramified, we determine when π(S,χ) is generic, and which generic characters it contains.