Refine listing
Actions for selected content:
352 results in 22Exx
Poles of L-functions and theta liftings for orthogonal groups
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 8 / Issue 4 / October 2009
- Published online by Cambridge University Press:
- 10 June 2009, pp. 693-741
- Print publication:
- October 2009
-
- Article
- Export citation
The Gelfand transform of homogeneous distributions on Heisenberg type groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 81 / Issue 3 / December 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 297-319
-
- Article
-
- You have access
- Export citation
Bilinear forms and 2-dimensional cohomology
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 41 / Issue 2 / October 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 165-179
-
- Article
-
- You have access
- Export citation
Theta functions on Hermitian symmetric domains and fock representations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 2 / April 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 201-234
-
- Article
-
- You have access
- Export citation
Convexity of generalized numerical range associated with a compact Lie group
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 1 / February 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 57-66
-
- Article
-
- You have access
- Export citation
An uncertainty principle like Hardy's theorem for nilpotent Lie groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 1 / August 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 47-54
-
- Article
-
- You have access
- Export citation
Distance to the convex hull of an orbit under the action of a compact Lie group
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 66 / Issue 3 / June 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 331-357
-
- Article
-
- You have access
- Export citation
On the Fourier transform of a compact semisimple Lie group
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 56 / Issue 1 / February 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 64-116
-
- Article
-
- You have access
- Export citation
Motion Groups and Absolutely Convergent Fourier Transforms
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 43 / Issue 3 / December 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 385-397
-
- Article
-
- You have access
- Export citation
The size of characters of exceptional lie groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 2 / October 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 233-248
-
- Article
-
- You have access
- Export citation
Cesàro kernels on classical groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 63 / Issue 3 / December 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 364-389
-
- Article
-
- You have access
- Export citation
Equivariant holomorphic maps into the Siegel disc and the metaplectic representation
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 62 / Issue 2 / April 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 160-174
-
- Article
-
- You have access
- Export citation
On the component group of the automorphism group of a Lie group
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 57 / Issue 3 / December 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 365-385
-
- Article
-
- You have access
- Export citation
Characterization of lipschitz spaces on compact Lie groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 58 / Issue 2 / April 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 200-209
-
- Article
-
- You have access
- Export citation
Lp-functions satisfying the mean value property on homogeneous spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 56 / Issue 3 / June 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 384-390
-
- Article
-
- You have access
- Export citation
A note on Riesz sets and lacunary sets
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 48 / Issue 1 / February 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 57-65
-
- Article
-
- You have access
- Export citation
The Plancherel formula for the horocycle space and generalizations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 61 / Issue 1 / August 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 42-56
-
- Article
-
- You have access
- Export citation
The Plancherel formula for the horocycle spaces and generalizations, II
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 65 / Issue 2 / October 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 194-211
-
- Article
-
- You have access
- Export citation
Weighted p-Sidon sets
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 61 / Issue 1 / August 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 73-95
-
- Article
-
- You have access
- Export citation
Subelliptic operators on Lie groups: regularity
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 57 / Issue 2 / October 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 179-229
-
- Article
-
- You have access
- Export citation
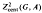 for certain 2-step nilpotent Lie groups
for certain 2-step nilpotent Lie groups 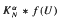 on the classical group
on the classical group 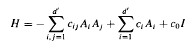
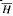 of
of 