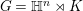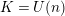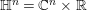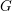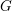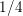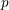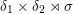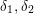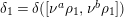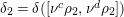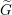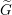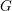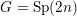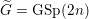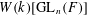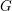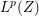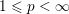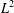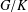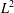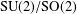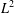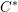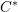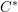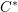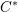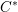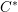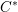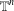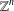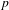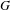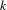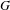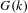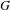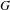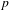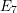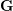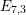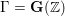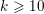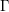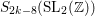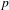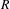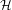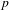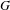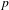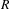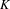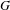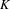Refine listing
Actions for selected content:
345 results in 22Exx
The affine Grassmannian and the Springer resolution in positive characteristic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 12 / December 2016
- Published online by Cambridge University Press:
- 28 November 2016, pp. 2627-2677
- Print publication:
- December 2016
-
- Article
- Export citation
MOVING FRAMES AND NOETHER’S CONSERVATION LAWS—THE GENERAL CASE
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 25 October 2016, e29
-
- Article
-
- You have access
- Open access
- Export citation
HARDY AND MIYACHI THEOREMS FOR HEISENBERG MOTION GROUPS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 229 / March 2018
- Published online by Cambridge University Press:
- 20 October 2016, pp. 1-20
- Print publication:
- March 2018
-
- Article
-
- You have access
- HTML
- Export citation
COMPOSITION FACTORS OF A CLASS OF INDUCED REPRESENTATIONS OF CLASSICAL
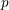 $p$ -ADIC GROUPS
$p$ -ADIC GROUPS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 227 / September 2017
- Published online by Cambridge University Press:
- 18 October 2016, pp. 16-48
- Print publication:
- September 2017
-
- Article
-
- You have access
- HTML
- Export citation
On a lifting problem of L-packets
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 9 / September 2016
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1800-1850
- Print publication:
- September 2016
-
- Article
- Export citation
Adjoint Orbits of Semi-Simple Lie Groups and Lagrangian Submanifolds
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 15 June 2016, pp. 361-385
-
- Article
- Export citation
THE BERNSTEIN CENTER OF THE CATEGORY OF SMOOTH
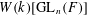 $W(k)[\text{GL}_{n}(F)]$ -MODULES
$W(k)[\text{GL}_{n}(F)]$ -MODULES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 07 June 2016, e11
-
- Article
-
- You have access
- Open access
- Export citation
Application of Lie Algebra in Constructing Volume-Preserving Algorithms for Charged Particles Dynamics
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 5 / May 2016
- Published online by Cambridge University Press:
- 17 May 2016, pp. 1397-1408
- Print publication:
- May 2016
-
- Article
- Export citation
SOLVABLE LIE GROUPS DEFINABLE IN O-MINIMAL THEORIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 28 April 2016, pp. 441-452
- Print publication:
- April 2018
-
- Article
- Export citation
Vanishing at infinity on homogeneous spaces of reductive type
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 7 / July 2016
- Published online by Cambridge University Press:
- 15 April 2016, pp. 1385-1397
- Print publication:
- July 2016
-
- Article
- Export citation
FUNCTORIAL ASPECTS OF THE RECONSTRUCTION OF LIE GROUPOIDS FROM THEIR BISECTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 101 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 14 March 2016, pp. 253-276
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
PERVERSE MOTIVES AND GRADED DERIVED CATEGORY
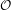 ${\mathcal{O}}$
${\mathcal{O}}$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 26 February 2016, pp. 347-395
- Print publication:
- April 2018
-
- Article
- Export citation
SMOOTHNESS OF CONVOLUTION PRODUCTS OF ORBITAL MEASURES ON RANK ONE COMPACT SYMMETRIC SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 12 February 2016, pp. 131-143
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
SYNTHETIC LIE THEORY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 10 February 2016, pp. 516-517
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
Parabolic induction and restriction via
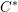 $C^{\ast }$-algebras and Hilbert
$C^{\ast }$-algebras and Hilbert 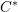 $C^{\ast }$-modules
$C^{\ast }$-modules
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 6 / June 2016
- Published online by Cambridge University Press:
- 02 February 2016, pp. 1286-1318
- Print publication:
- June 2016
-
- Article
- Export citation
MAXIMAL SEMIGROUP SYMMETRY AND DISCRETE RIESZ TRANSFORMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 14 December 2015, pp. 216-240
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
FROM THE FUNCTION-SHEAF DICTIONARY TO QUASICHARACTERS OF
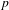 $p$ -ADIC TORI
$p$ -ADIC TORI
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 13 October 2015, pp. 1-37
- Print publication:
- February 2018
-
- Article
- Export citation
ON THE LOCAL LANGLANDS CORRESPONDENCE FOR SPLIT CLASSICAL GROUPS OVER LOCAL FUNCTION FIELDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 16 / Issue 5 / November 2017
- Published online by Cambridge University Press:
- 30 September 2015, pp. 987-1074
- Print publication:
- November 2017
-
- Article
- Export citation
Cusp forms on the exceptional group of type
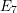 $E_{7}$
$E_{7}$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 2 / February 2016
- Published online by Cambridge University Press:
- 07 September 2015, pp. 223-254
- Print publication:
- February 2016
-
- Article
- Export citation
THE PRO-p-IWAHORI HECKE ALGEBRA OF A REDUCTIVE p-ADIC GROUP III (SPHERICAL HECKE ALGEBRAS AND SUPERSINGULAR MODULES)
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 16 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 03 June 2015, pp. 571-608
- Print publication:
- June 2017
-
- Article
- Export citation