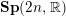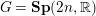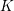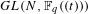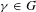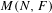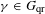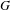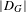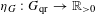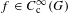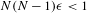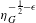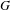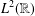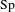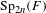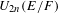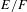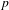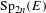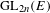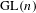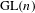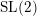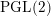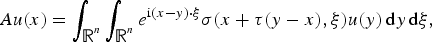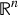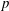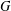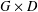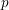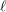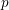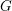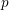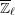Refine listing
Actions for selected content:
345 results in 22Exx
SUR LES PAQUETS D’ARTHUR DE
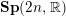 $\mathbf{Sp}(2n,\mathbb{R})$ CONTENANT DES MODULES UNITAIRES DE PLUS HAUT POIDS, SCALAIRES
$\mathbf{Sp}(2n,\mathbb{R})$ CONTENANT DES MODULES UNITAIRES DE PLUS HAUT POIDS, SCALAIRES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 241 / March 2021
- Published online by Cambridge University Press:
- 13 June 2019, pp. 44-124
- Print publication:
- March 2021
-
- Article
- Export citation
Local-global principles in circle packings
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 6 / June 2019
- Published online by Cambridge University Press:
- 20 May 2019, pp. 1118-1170
- Print publication:
- June 2019
-
- Article
- Export citation
INTÉGRALES ORBITALES SUR
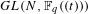 $GL(N,\mathbb{F}_{q}((t)))$
$GL(N,\mathbb{F}_{q}((t)))$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 2 / March 2021
- Published online by Cambridge University Press:
- 14 May 2019, pp. 423-515
- Print publication:
- March 2021
-
- Article
- Export citation
A RESULT OF PALEY AND WIENER ON DAMEK–RICCI SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 03 May 2019, pp. 1-16
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
A support theorem for the X-ray transform on manifolds with plane covers
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 1 / July 2020
- Published online by Cambridge University Press:
- 25 April 2019, pp. 149-158
- Print publication:
- July 2020
-
- Article
- Export citation
ON
 $\text{Sp}$-DISTINGUISHED REPRESENTATIONS OF THE QUASI-SPLIT UNITARY GROUPS
$\text{Sp}$-DISTINGUISHED REPRESENTATIONS OF THE QUASI-SPLIT UNITARY GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 17 April 2019, pp. 225-276
- Print publication:
- January 2021
-
- Article
- Export citation
PARITY OF THE LANGLANDS PARAMETERS OF CONJUGATE SELF-DUAL REPRESENTATIONS OF
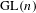 $\text{GL}(n)$ AND THE LOCAL JACQUET–LANGLANDS CORRESPONDENCE
$\text{GL}(n)$ AND THE LOCAL JACQUET–LANGLANDS CORRESPONDENCE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 19 February 2019, pp. 2017-2043
- Print publication:
- November 2020
-
- Article
- Export citation
Geometric Langlands correspondence for
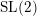 $\text{SL}(2)$,
$\text{SL}(2)$, 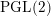 $\text{PGL}(2)$ over the pair of pants
$\text{PGL}(2)$ over the pair of pants
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 2 / February 2019
- Published online by Cambridge University Press:
- 07 February 2019, pp. 324-371
- Print publication:
- February 2019
-
- Article
- Export citation
Pseudo-differential operators with nonlinear quantizing functions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 23 January 2019, pp. 103-130
- Print publication:
- February 2020
-
- Article
-
- You have access
- Open access
- Export citation
Lipschitz 1-connectedness for Some Solvable Lie Groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 533-555
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
Eisenstein Series Arising from Jordan Algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 09 January 2019, pp. 183-201
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
Models of Representations and Langlands Functoriality
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 07 January 2019, pp. 676-707
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
Completeness of Infinite-dimensional Lie Groups in Their Left Uniformity
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 131-152
- Print publication:
- February 2019
-
- Article
-
- You have access
- Open access
- Export citation
Casselman’s Basis of Iwahori Vectors and Kazhdan–Lusztig Polynomials
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 1351-1366
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
Finsler Warped Product Metrics of Douglas Type
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 1 / March 2019
- Published online by Cambridge University Press:
- 04 January 2019, pp. 119-130
- Print publication:
- March 2019
-
- Article
-
- You have access
- Export citation
Explicit asymptotic expansions for tame supercuspidal characters
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 11 / November 2018
- Published online by Cambridge University Press:
- 12 October 2018, pp. 2305-2378
- Print publication:
- November 2018
-
- Article
- Export citation
HARDY’S THEOREM FOR GABOR TRANSFORM
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 106 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 15 August 2018, pp. 143-159
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
Nearby cycles of Whittaker sheaves on Drinfeld’s compactification
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 8 / August 2018
- Published online by Cambridge University Press:
- 18 July 2018, pp. 1775-1800
- Print publication:
- August 2018
-
- Article
- Export citation
INTERTWINING SEMISIMPLE CHARACTERS FOR
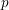 $p$-ADIC CLASSICAL GROUPS
$p$-ADIC CLASSICAL GROUPS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 238 / June 2020
- Published online by Cambridge University Press:
- 16 July 2018, pp. 137-205
- Print publication:
- June 2020
-
- Article
-
- You have access
- HTML
- Export citation
Sur les
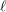 $\ell$ -blocs de niveau zéro des groupes
$\ell$ -blocs de niveau zéro des groupes 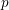 $p$ -adiques
$p$ -adiques
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 7 / July 2018
- Published online by Cambridge University Press:
- 24 May 2018, pp. 1473-1507
- Print publication:
- July 2018
-
- Article
- Export citation