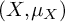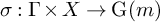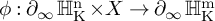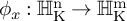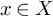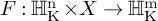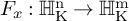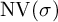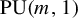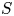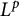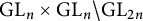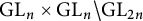Refine listing
Actions for selected content:
345 results in 22Exx
Fundamental local equivalences in quantum geometric Langlands
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 27 December 2021, pp. 2699-2732
- Print publication:
- December 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TRUNCATED AFFINE SPRINGER FIBERS AND ARTHUR’S WEIGHTED ORBITAL INTEGRALS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 10 November 2021, pp. 1757-1818
- Print publication:
- July 2023
-
- Article
- Export citation
Exponential mixing of frame flows for convex cocompact hyperbolic manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 08 November 2021, pp. 2585-2634
- Print publication:
- December 2021
-
- Article
- Export citation
Steenrod operators, the Coulomb branch and the Frobenius twist
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 04 November 2021, pp. 2494-2552
- Print publication:
- November 2021
-
- Article
- Export citation
Effective equidistribution for generalized higher-step nilflows
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 12 / December 2022
- Published online by Cambridge University Press:
- 25 October 2021, pp. 3656-3715
- Print publication:
- December 2022
-
- Article
- Export citation
Boundary maps and maximal representations on infinite-dimensional Hermitian symmetric spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 18 October 2021, pp. 140-189
- Print publication:
- January 2023
-
- Article
- Export citation
On holomorphic reflexivity conditions for complex Lie groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 4 / November 2021
- Published online by Cambridge University Press:
- 30 September 2021, pp. 800-821
-
- Article
- Export citation
NATURAL MAPS FOR MEASURABLE COCYCLES OF COMPACT HYPERBOLIC MANIFOLDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 29 September 2021, pp. 421-448
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An arithmetic property of intertwining operators for p-adic groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 17 September 2021, pp. 83-107
- Print publication:
- February 2023
-
- Article
- Export citation
Multiplicative constants and maximal measurable cocycles in bounded cohomology
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 11 / November 2022
- Published online by Cambridge University Press:
- 31 August 2021, pp. 3490-3525
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Annihilator varieties of distinguished modules of reductive Lie algebras
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 26 July 2021, e52
-
- Article
-
- You have access
- Open access
- Export citation
A construction of complex analytic elliptic cohomology from double free loop spaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 8 / August 2021
- Published online by Cambridge University Press:
- 26 July 2021, pp. 1853-1897
- Print publication:
- August 2021
-
- Article
- Export citation
Diagrams in the mod p cohomology of Shimura curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 8 / August 2021
- Published online by Cambridge University Press:
- 07 July 2021, pp. 1653-1723
- Print publication:
- August 2021
-
- Article
- Export citation
Corrigendum: On the cuspidal cohomology of S-arithmetic subgroups of reductive groups over number fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 6 / June 2021
- Published online by Cambridge University Press:
- 26 May 2021, pp. 1207-1210
- Print publication:
- June 2021
-
- Article
-
- You have access
- HTML
- Export citation
Oscillating multipliers on symmetric and locally symmetric spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 14 May 2021, pp. 887-905
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Geodesic planes in geometrically finite acylindrical
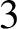 $3$-manifolds
$3$-manifolds
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 04 May 2021, pp. 514-553
- Print publication:
- February 2022
-
- Article
- Export citation
THE SMOOTHNESS OF ORBITAL MEASURES ON NONCOMPACT SYMMETRIC SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 26 April 2021, pp. 188-207
- Print publication:
- October 2022
-
- Article
- Export citation
ON FORMAL DEGREES OF UNIPOTENT REPRESENTATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 19 March 2021, pp. 1947-1999
- Print publication:
- November 2022
-
- Article
- Export citation
R-GROUP AND WHITTAKER SPACE OF SOME GENUINE REPRESENTATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 08 March 2021, pp. 213-273
- Print publication:
- January 2023
-
- Article
- Export citation
Orbital integrals on
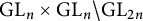 $\text{GL}_n \times \text{GL}_n \backslash \text{GL}_{2n}$
$\text{GL}_n \times \text{GL}_n \backslash \text{GL}_{2n}$
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 26 February 2021, pp. 858-886
- Print publication:
- June 2022
-
- Article
- Export citation