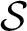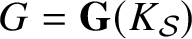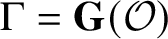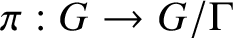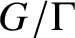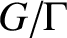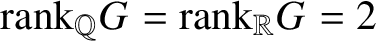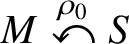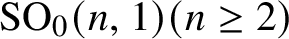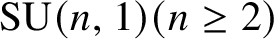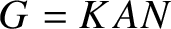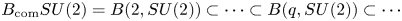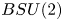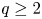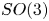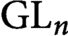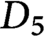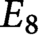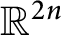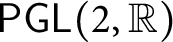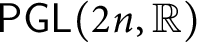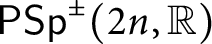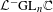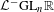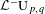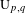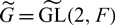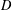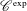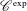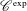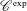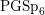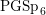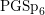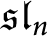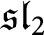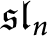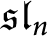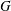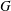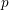Refine listing
Actions for selected content:
345 results in 22Exx
Le transfert singulier pour la formule des traces de Jacquet–Rallis
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 16 March 2021, pp. 303-434
- Print publication:
- February 2021
-
- Article
- Export citation
ON A CERTAIN LOCAL IDENTITY FOR LAPID–MAO’S CONJECTURE AND FORMAL DEGREE CONJECTURE : EVEN UNITARY GROUP CASE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 08 January 2021, pp. 1107-1161
- Print publication:
- July 2022
-
- Article
- Export citation
Closures of locally divergent orbits of maximal tori and values of homogeneous forms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 05 November 2020, pp. 3142-3177
- Print publication:
- October 2021
-
- Article
- Export citation
Divergent trajectories in arithmetic homogeneous spaces of rational rank two
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 05 November 2020, pp. 3116-3141
- Print publication:
- October 2021
-
- Article
-
- You have access
- Open access
- Export citation
Vanishing of cohomology and parameter rigidity of actions of solvable Lie groups, II
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 03 November 2020, pp. 3023-3059
- Print publication:
- October 2021
-
- Article
-
- You have access
- Open access
- Export citation
Sup-norms of eigenfunctions in the level aspect for compact arithmetic surfaces, II: newforms and subconvexity
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 11 / November 2020
- Published online by Cambridge University Press:
- 15 December 2020, pp. 2368-2398
- Print publication:
- November 2020
-
- Article
- Export citation
Branching laws for classical groups: the non-tempered case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 11 / November 2020
- Published online by Cambridge University Press:
- 17 December 2020, pp. 2298-2367
- Print publication:
- November 2020
-
- Article
- Export citation
Nilpotent n-tuples in SU(2)
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 4 / November 2020
- Published online by Cambridge University Press:
- 30 September 2020, pp. 1005-1030
-
- Article
- Export citation
Arithmeticity of discrete subgroups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 9 / September 2021
- Published online by Cambridge University Press:
- 28 September 2020, pp. 2561-2590
- Print publication:
- September 2021
-
- Article
- Export citation
Fourier coefficients of minimal and next-to-minimal automorphic representations of simply-laced groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 21 September 2020, pp. 122-169
- Print publication:
- February 2022
-
- Article
-
- You have access
- Open access
- Export citation
Rigidity of diagonally embedded triangle groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 20 August 2020, pp. 560-579
- Print publication:
- September 2021
-
- Article
- Export citation
PROJECTIVE LOOPS GENERATE RATIONAL LOOP GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 17 August 2020, pp. 459-485
- Print publication:
- March 2022
-
- Article
- Export citation
DUALIZING INVOLUTIONS ON THE METAPLECTIC GL(2) à la TUPAN
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 10 July 2020, pp. 426-437
- Print publication:
- May 2021
-
- Article
- Export citation
WAVE FRONT HOLONOMICITY OF
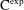 $\text{C}^{\text{exp}}$-CLASS DISTRIBUTIONS ON NON-ARCHIMEDEAN LOCAL FIELDS
$\text{C}^{\text{exp}}$-CLASS DISTRIBUTIONS ON NON-ARCHIMEDEAN LOCAL FIELDS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 30 June 2020, e35
-
- Article
-
- You have access
- Open access
- Export citation
DISTAL ACTIONS OF AUTOMORPHISMS OF NILPOTENT GROUPS G ON SUBG AND APPLICATIONS TO LATTICES IN LIE GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 23 June 2020, pp. 343-362
- Print publication:
- May 2021
-
- Article
- Export citation
An exceptional Siegel–Weil formula and poles of the Spin L-function of
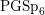 $\text{PGSp}_{6}$
$\text{PGSp}_{6}$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 6 / June 2020
- Published online by Cambridge University Press:
- 29 May 2020, pp. 1231-1261
- Print publication:
- June 2020
-
- Article
- Export citation
Categorification via blocks of modular representations for
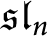 $\mathfrak {sl}_n$
$\mathfrak {sl}_n$
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 19 May 2020, pp. 1095-1123
- Print publication:
- August 2021
-
- Article
-
- You have access
- Open access
- Export citation
Données endoscopiques d’un groupe réductif connexe : applications d’une construction de Langlands
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 15 May 2020, pp. 1074-1094
- Print publication:
- August 2021
-
- Article
- Export citation
Finsler Warped Product Metrics with Relatively Isotropic Landsberg Curvature
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 12 May 2020, pp. 182-191
- Print publication:
- March 2021
-
- Article
- Export citation
Local Rankin–Selberg integrals for Speh representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 5 / May 2020
- Published online by Cambridge University Press:
- 13 April 2020, pp. 908-945
- Print publication:
- May 2020
-
- Article
-
- You have access
- Open access
- HTML
- Export citation