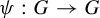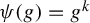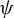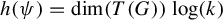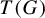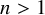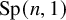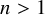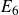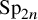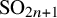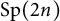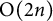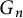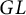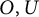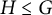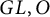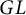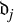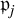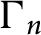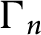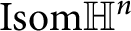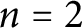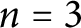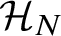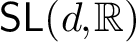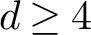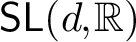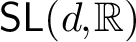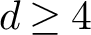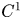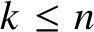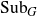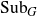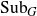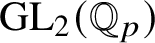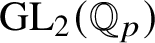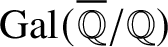Refine listing
Actions for selected content:
345 results in 22Exx
STRUCTURAL STABILITY OF MEANDERING-HYPERBOLIC GROUP ACTIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 27 December 2022, pp. 753-810
- Print publication:
- March 2024
-
- Article
- Export citation
The topological entropy of powers on Lie groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 11 / November 2023
- Published online by Cambridge University Press:
- 13 December 2022, pp. 3726-3744
- Print publication:
- November 2023
-
- Article
- Export citation
Local newforms for the general linear groups over a non-archimedean local field
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 13 December 2022, e24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quaternionic hyperbolic lattices of minimal covolume
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 25 August 2022, e68
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the profinite rigidity of lattices in higher rank Lie groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 22 August 2022, pp. 369-384
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Effective equidistribution of horospherical flows in infinite volume rank-one homogeneous spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 8 / August 2023
- Published online by Cambridge University Press:
- 09 August 2022, pp. 2780-2840
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quasi-solvable lattice models for
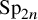 $\operatorname {Sp}_{2n}$ and
$\operatorname {Sp}_{2n}$ and 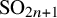 $\operatorname {SO}_{2n+1}$ Demazure atoms and characters
$\operatorname {SO}_{2n+1}$ Demazure atoms and characters
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 18 July 2022, e53
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Gelfand–Graev representation of classical groups in terms of Hecke algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 24 June 2022, pp. 1343-1368
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Multiplicity one theorems over positive characteristic
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 22 June 2022, pp. 1018-1044
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Geometric orbital integrals and the center of the enveloping algebra
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 6 / June 2022
- Published online by Cambridge University Press:
- 11 August 2022, pp. 1189-1253
- Print publication:
- June 2022
-
- Article
- Export citation
COMPLEX STRUCTURES ON STRATIFIED LIE ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 19 April 2022, pp. 320-332
- Print publication:
- October 2022
-
- Article
- Export citation
Hyperbolic Coxeter groups of minimal growth rates in higher dimensions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 06 April 2022, pp. 232-242
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An operadic approach to substitution in Lie–Butcher series
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 31 March 2022, e20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
QUASI-ISOMETRIC EMBEDDINGS INAPPROXIMABLE BY ANOSOV REPRESENTATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 14 March 2022, pp. 2497-2514
- Print publication:
- September 2023
-
- Article
- Export citation
C1 actions on manifolds by lattices in Lie groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 13 May 2022, pp. 529-549
- Print publication:
- March 2022
-
- Article
- Export citation
Lipschitz graphs and currents in Heisenberg groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 02 February 2022, e6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NOTE ON ÉTALE REPRESENTATIONS FROM NILPOTENT ORBITS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 25 January 2022, pp. 113-125
- Print publication:
- August 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Distal Actions of Automorphisms of Lie Groups G on SubG
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 2 / September 2022
- Published online by Cambridge University Press:
- 21 December 2021, pp. 457-478
- Print publication:
- September 2022
-
- Article
- Export citation
Finiteness properties of the category of mod p representations of
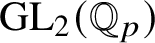 ${\textrm {GL}}_2 (\mathbb {Q}_{p})$
${\textrm {GL}}_2 (\mathbb {Q}_{p})$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 09 December 2021, e80
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the construction of tame supercuspidal representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 03 January 2022, pp. 2733-2746
- Print publication:
- December 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation