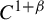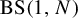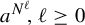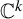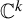Contents
Original Article
Dynamical degrees of affine-triangular automorphisms of affine spaces
- Part of:
-
- Published online by Cambridge University Press:
- 01 October 2021, pp. 3551-3592
-
- Article
- Export citation
Smoothness of stable holonomies inside center-stable manifolds
- Part of:
-
- Published online by Cambridge University Press:
- 18 October 2021, pp. 3593-3618
-
- Article
- Export citation
Analytic classification of germs of parabolic antiholomorphic diffeomorphisms of codimension k
- Part of:
-
- Published online by Cambridge University Press:
- 30 September 2021, pp. 3619-3655
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Effective equidistribution for generalized higher-step nilflows
- Part of:
-
- Published online by Cambridge University Press:
- 25 October 2021, pp. 3656-3715
-
- Article
- Export citation
Glider automata on all transitive sofic shifts
- Part of:
-
- Published online by Cambridge University Press:
- 30 September 2021, pp. 3716-3744
-
- Article
- Export citation
Excursions to the cusps for geometrically finite hyperbolic orbifolds and equidistribution of closed geodesics in regular covers
- Part of:
-
- Published online by Cambridge University Press:
- 15 November 2021, pp. 3745-3791
-
- Article
- Export citation
Subshifts and colorings on ascending HNN-extensions of finitely generated abelian groups
- Part of:
-
- Published online by Cambridge University Press:
- 08 September 2021, pp. 3792-3817
-
- Article
- Export citation
Exponential mixing property for Hénon–Sibony maps of
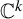 $\mathbb {C}^k$
$\mathbb {C}^k$
-
- Published online by Cambridge University Press:
- 17 September 2021, pp. 3818-3830
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
ETS volume 42 issue 12 Cover and Front matter
-
- Published online by Cambridge University Press:
- 04 November 2022, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
ETS volume 42 issue 12 Cover and Back matter
-
- Published online by Cambridge University Press:
- 04 November 2022, pp. b1-b2
-
- Article
-
- You have access
- Export citation