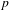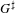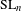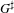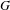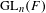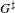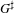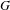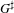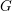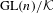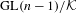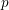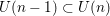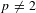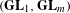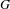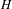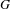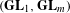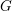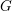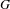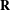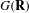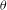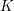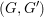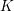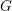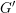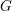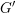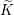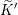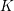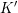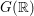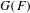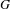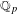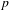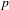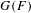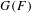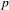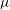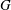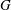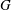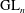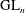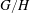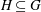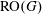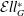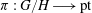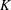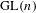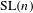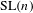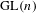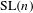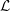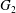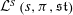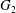Refine listing
Actions for selected content:
345 results in 22Exx
HECKE ALGEBRAS FOR INNER FORMS OF
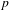 $p$ -ADIC SPECIAL LINEAR GROUPS
$p$ -ADIC SPECIAL LINEAR GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 16 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 05 May 2015, pp. 351-419
- Print publication:
- April 2017
-
- Article
- Export citation
Elliptic Springer theory
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 8 / August 2015
- Published online by Cambridge University Press:
- 08 April 2015, pp. 1568-1584
- Print publication:
- August 2015
-
- Article
- Export citation
WHITTAKER PERIODS, MOTIVIC PERIODS, AND SPECIAL VALUES OF TENSOR PRODUCT
 $L$ -FUNCTIONS
$L$ -FUNCTIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 4 / October 2016
- Published online by Cambridge University Press:
- 31 March 2015, pp. 711-769
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
Endoscopie et conjecture locale raffinée de Gan–Gross–Prasad pour les groupes unitaires
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 7 / July 2015
- Published online by Cambridge University Press:
- 18 February 2015, pp. 1309-1371
- Print publication:
- July 2015
-
- Article
- Export citation
GEOMETRIC TAMELY RAMIFIED LOCAL THETA CORRESPONDENCE IN THE FRAMEWORK OF THE GEOMETRIC LANGLANDS PROGRAM
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 3 / July 2016
- Published online by Cambridge University Press:
- 18 February 2015, pp. 625-671
- Print publication:
- July 2016
-
- Article
- Export citation
Diophantine properties of nilpotent Lie groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 6 / June 2015
- Published online by Cambridge University Press:
- 13 January 2015, pp. 1157-1188
- Print publication:
- June 2015
-
- Article
- Export citation
LINEAR AND PROJECTIVE BOUNDARY OF NILPOTENT GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 22 December 2014, pp. 591-632
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
KILLING FRAMES AND S-CURVATURE OF HOMOGENEOUS FINSLER SPACES*
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 2 / May 2015
- Published online by Cambridge University Press:
- 22 December 2014, pp. 457-464
- Print publication:
- May 2015
-
- Article
-
- You have access
- Export citation
TEMPERED SPECTRAL TRANSFER IN THE TWISTED ENDOSCOPY OF REAL GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 3 / July 2016
- Published online by Cambridge University Press:
- 17 December 2014, pp. 569-612
- Print publication:
- July 2016
-
- Article
- Export citation
A study of the representations supported by the orbit closure of the determinant
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 2 / February 2015
- Published online by Cambridge University Press:
- 24 October 2014, pp. 292-312
- Print publication:
- February 2015
-
- Article
- Export citation
Invariants and
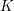 $K$-spectrums of local theta lifts
$K$-spectrums of local theta lifts
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 17 September 2014, pp. 179-206
- Print publication:
- January 2015
-
- Article
- Export citation
The real Chevalley involution
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 12 / December 2014
- Published online by Cambridge University Press:
- 27 August 2014, pp. 2127-2142
- Print publication:
- December 2014
-
- Article
- Export citation
EXTENSIONS ENTRE SÉRIES PRINCIPALES
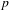 $p$-ADIQUES ET MODULO
$p$-ADIQUES ET MODULO 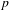 $p$ DE
$p$ DE 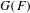 $G(F)$
$G(F)$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 08 August 2014, pp. 225-270
- Print publication:
- April 2016
-
- Article
- Export citation
SUR LE COMPTAGE DES FIBRÉS DE HITCHIN NILPOTENTS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 07 August 2014, pp. 91-164
- Print publication:
- January 2016
-
- Article
-
- You have access
- Export citation
Random walks on projective spaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 9 / September 2014
- Published online by Cambridge University Press:
- 17 July 2014, pp. 1579-1606
- Print publication:
- September 2014
-
- Article
- Export citation
Raising the level for
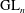 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\text {GL}_{{n}}$
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\text {GL}_{{n}}$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 2 / 01 July 2014
- Published online by Cambridge University Press:
- 10 June 2014, e16
-
- Article
-
- You have access
- Open access
- Export citation
SUPERBOSONIZATION VIA RIESZ SUPERDISTRIBUTIONS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 2 / 01 July 2014
- Published online by Cambridge University Press:
- 14 May 2014, e9
-
- Article
-
- You have access
- Open access
- Export citation
The elliptic Weyl character formula
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 7 / July 2014
- Published online by Cambridge University Press:
- 12 May 2014, pp. 1196-1234
- Print publication:
- July 2014
-
- Article
- Export citation
LIMIT MULTIPLICITIES FOR PRINCIPAL CONGRUENCE SUBGROUPS OF
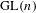 $\text{GL}(n)$ AND
$\text{GL}(n)$ AND 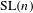 $\text{SL}(n)$
$\text{SL}(n)$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 14 / Issue 3 / July 2015
- Published online by Cambridge University Press:
- 08 May 2014, pp. 589-638
- Print publication:
- July 2015
-
- Article
- Export citation
The Rankin–Selberg integral with a non-unique model for the standard
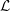 $\mathcal{L}$ -function of
$\mathcal{L}$ -function of 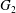 $G_2$
$G_2$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 14 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 08 May 2014, pp. 149-184
- Print publication:
- January 2015
-
- Article
- Export citation