In this section we discuss a very simple problem. Consider the scalar initial value problem

Here ε > 0 is a small constant and a = a1 + ia2, a1, a2 real, is a complex number with |a| = 1. We can write down the solution of (1.1) explicity. It is

where

is the forced solution and

is a solution of the homogeneous equation

yS varies on the time scale ‘1’ while yF varies on the much faster scale 1/ε. We say that yS, yF vary on the slow and fast scale, respectively. We use also the phrase: yS and yF are the slow and the fast part of the solution, respectively.

It used to be good enough to bound absolute of matrix eigenvalues and singular values. Not any more. Now it is fashionable to bound relative errors. We present a collection of relative perturbation results which have emerged during the past ten years.

No need to throw away all those absolute error bound, though. Deep down, the derivation of many relative bounds can be based on absolute bounds. This means that relative bounds are not always better. They may just be better sometimes – and exactly when depends on the perturbation.

Recent advances in the field of iterative methods for solving large linear systems are reviewed. The main focus is on developments in the area of conjugate gradient-type algorithms and Krylov subspace methods for nonHermitian matrices.

Let P(x) = 0 be a system of n polynomial equations in n unknowns. Denoting P = (p1,…, pn), we want to find all isolated solutions of

for x = (x1,…,xn). This problem is very common in many fields of science and engineering, such as formula construction, geometric intersection problems, inverse kinematics, power flow problems with PQ-specified bases, computation of equilibrium states, etc. Elimination theory-based methods, most notably the Buchberger algorithm (Buchberger 1985) for constructing Gröbner bases, are the classical approach to solving (1.1), but their reliance on symbolic manipulation makes those methods seem somewhat unsuitable for all but small problems.

From the fundamental laws of elasticity, we write a model for the contact between two membranes and we perform the analysis of the corresponding system of variational inequalities. We propose a finite element discretization of this problem and prove its well-posedness. We also establish a priori and a posteriori error estimates.

This article deals with the numerical computation of the Cheeger constant and the approximation of the maximal Cheeger set of a given subset of ${\mathbb R}^d$ . This problem is motivated by landslide modelling as well as by the continuous maximal flow problem. Using the fact that the maximal Cheeger set can be approximated by solving a rather simple projection problem, we propose a numerical strategy to compute maximal Cheeger sets and Cheeger constants.

This paper is devoted to the numerical solution of stationarylaminar Bingham fluids by path-following methods. By using duality theory, asystem that characterizes the solution of the original problem is derived.Since this system is ill-posed, a family of regularized problems is obtainedand the convergence of the regularized solutions to the original one is proved.For the update of the regularization parameter, a path-following method isinvestigated. Based on the differentiability properties of the path, a model ofthe value functional and a correspondent algorithm are constructed. For thesolution of the systems obtained in each path-following iteration a semismoothNewton method is proposed. Numerical experiments are performed in order toinvestigate the behavior and efficiency of the method, and a comparison with apenalty-Newton-Uzawa-conjugate gradient method, proposed in [Dean et al., J. Non-Newtonian Fluid Mech.142 (2007) 36–62], iscarried out.

We propose here a model and a numerical scheme to compute the motionof rigid particles interacting through the lubrication force. In thecase of a particle approaching a plane, we propose an algorithm andprove its convergence towards the solutions to the gluey particle modeldescribed in [B. Maury, ESAIM: Proceedings18 (2007)133–142]. We propose a multi-particle version ofthis gluey model which is based on the projection of the velocitiesonto a set of admissible velocities. Then, we describe a multi-particle algorithmfor the simulation of such systems and present numerical results.

The powerful Hamilton-Jacobi theory is used for constructing regularizations and error estimates for optimal design problems. The constructed Pontryagin method is a simple and general method for optimal design and reconstruction: the first, analytical, step is to regularize the Hamiltonian; next the solution to its stationary Hamiltonian system, a nonlinear partial differential equation, is computed with the Newton method. The method is efficient for designs where the Hamiltonian function can be explicitly formulated and when the Jacobian is sparse, but becomes impractical otherwise (e.g. for non local control constraints). An error estimate for the difference between exact and approximate objective functions is derived, depending only on the difference of the Hamiltonian and its finite dimensional regularization along the solution path and its L2 projection, i.e. not on the difference of the exact and approximate solutions to the Hamiltonian systems.

This note explains the circumstances under which a type 〈1〉 quantifier can be decomposed into a type 〈1, 1〉 quantifier and a set, by fixing the first argument of the former to the latter. The motivation comes from the semantics of Noun Phrases (also called Determiner Phrases) in natural languages, but in this article, I focus on the logical facts. However, my examples are taken among quantifiers appearing in natural languages, and at the end, I sketch two more principled linguistic applications.

Public announcement logic is an extension of multiagent epistemic logic with dynamic operators to model the informational consequences of announcements to the entire group of agents. We propose an extension of public announcement logic with a dynamic modal operator that expresses what is true after any announcement: ⋄φ expresses that there is a truthful announcement ψ after which φ is true. This logic gives a perspective on Fitch's knowability issues: For which formulas φ, does it hold that φ → ⋄Kφ? We give various semantic results and show completeness for a Hilbert-style axiomatization of this logic. There is a natural generalization to a logic for arbitrary events.

Steve Awodey and Kohei Kishida (2008). Topology and Modality: The Topological Interpretation of First-Order Modal Logic. The Review of Symbolic Logic 1(2): 146-166.

On page 148 of this article an error was introduced during the production process. The final equation in the displayed formula 8 lines from the bottom of the page should read,

[0, 1) ≠ [0, 1]

The publisher regrets this error.

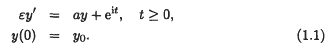
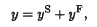
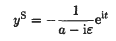
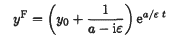
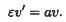
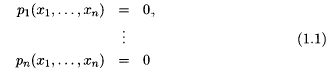
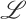In this article, we propose a belief revision approach for families of (non-classical) logics whose semantics are first-order axiomatisable. Given any such (non-classical) logic , the approach enables the definition of belief revision operators for 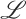, in terms of a belief revision operation satisfying the postulates for revision theory proposed by Alchourrón, Gärdenfors and Makinson (AGM revision, Alchourrón et al. (1985)). The approach is illustrated by considering the modal logic K, Belnap's four-valued logic, and Łukasiewicz's many-valued logic. In addition, we present a general methodology to translate algebraic logics into classical logic. For the examples provided, we analyse in what circumstances the properties of the AGM revision are preserved and discuss the advantages of the approach from both theoretical and practical viewpoints.

Argument-places play an important role in our dealing with relations. However, that does not mean that argument-places should be taken as primitive entities. It is possible to give an account of ‘real’ relations in which argument-places play no role. But if argument-places are not basic, then what can we say about their identity? Can they, for example, be reconstructed in set theory with appropriate urelements? In this article, we show that for some relations, argument-places cannot be modeled in a neutral way in V[A], the cumulative hierarchy with basic ingredients of the relation as urelements. We argue that a natural way to conceive of argument-places is to identify them with abstract, structureless points of a derivative structure exemplified by positional frames. In case the relation has symmetry, these points may be indiscernible.

For nonmonotonic logics, Cumulativity is an important logical rule. We show here that Cumulativity fans out into an infinity of different conditions, if the domain is not closed under finite unions.

In this work, we consider dynamic frictionless contact with adhesionbetween a viscoelastic body of the Kelvin-Voigt type and astationary rigid obstacle, based on the Signorini's contact conditions.Including the adhesion processes modeled by the bonding field, a newversion of energy function is defined. We use the energy functionto derive a new form of energy balance which is supported by numericalresults. Employing the time-discretization, we establish a numerical formulation and investigate the convergence of numerical trajectories. The fullydiscrete approximation which satisfies the complementarity conditionsis computed by using the nonsmooth Newton's method with the Kanzow-Kleinmichelfunction. Numerical simulations of a viscoelastic beam clamped attwo ends are presented.

The main objective of this paper is to provenew necessary conditions to the existence ofKAM tori. To do so, we develop a set ofexplicit a-priori estimates for smoothsolutions of Hamilton-Jacobi equations,using a combination of methods fromviscosity solutions,KAM and Aubry-Mather theories.These estimatesare validin anyspace dimension, and can be checked numericallyto detect gaps between KAM tori and Aubry-Mather sets.We apply these results to detect non-integrable regions in several examples such as a forced pendulum, two coupled penduli, andthe double pendulum.

This paper is concerned with numerical methods for compressible multicomponent fluids. The fluid components are assumed immiscible, and areseparated by material interfaces, each endowed with its own equation of state (EOS). Cell averages of computational cells that are occupiedby several fluid components require a “mixed-cell” EOS, which may not always be physically meaningful, and often leads to spurious oscillations. We present a new interface tracking algorithm, which avoids using mixed-cell information by solving the Riemann problembetween its single-fluid neighboring cells. The resulting algorithm is oscillation-free for isolated material interfaces, conservative, andtends to produce almost perfect jumps across material fronts. The computational framework is general and may be used in conjunction withone's favorite finite-volume method. The robustness of the method is illustrated on shock-interface interaction in one space dimension,oscillating bubbles with radial symmetry and shock-bubble interaction in two space dimensions.

The Ultra Weak Variational Formulation (UWVF) of the Helmholtz equationprovides a variational framework suitable for discretization using plane wave solutionsof an appropriate adjoint equation. Currently convergence of the method is only proved on the boundary of the domain. However substantial computational evidence exists showing that the method also converges throughout the domain of the Helmholtz equation. In this paper we exploit the fact that the UWVF is essentially an upwind discontinuous Galerkin method to prove convergence of the solution in the special case where there is no absorbing medium present. We also provide some other estimates in the case when absorption is present, and give some simple numerical results to test the estimates. We expect that similar techniques can be used to prove error estimates for the UWVF applied to Maxwell's equations and elasticity.