Refine search
Actions for selected content:
4288 results in Numerical analysis and computational science
Numerical analysisof a frictionless viscoelastic piezoelectric contact problem
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 42 / Issue 4 / July 2008
- Published online by Cambridge University Press:
- 05 June 2008, pp. 667-682
- Print publication:
- July 2008
-
- Article
- Export citation
Numerical solution of a 1-d elastohydrodynamic problemin magnetic storage devices
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 42 / Issue 4 / July 2008
- Published online by Cambridge University Press:
- 05 June 2008, pp. 645-665
- Print publication:
- July 2008
-
- Article
- Export citation
An entropy satisfying scheme for two-layer shallow water equations with uncoupled treatment
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 42 / Issue 4 / July 2008
- Published online by Cambridge University Press:
- 05 June 2008, pp. 683-698
- Print publication:
- July 2008
-
- Article
- Export citation
THE ITERATIVE CONCEPTION OF SET
-
- Journal:
- The Review of Symbolic Logic / Volume 1 / Issue 1 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 97-110
- Print publication:
- June 2008
-
- Article
- Export citation
HOW APPLIED MATHEMATICS BECAME PURE
-
- Journal:
- The Review of Symbolic Logic / Volume 1 / Issue 1 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 16-41
- Print publication:
- June 2008
-
- Article
- Export citation
PROBABILISTIC CONDITIONALS ARE ALMOST MONOTONIC
-
- Journal:
- The Review of Symbolic Logic / Volume 1 / Issue 1 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 73-80
- Print publication:
- June 2008
-
- Article
- Export citation
ON ADOPTING KRIPKE SEMANTICS IN SET THEORY
-
- Journal:
- The Review of Symbolic Logic / Volume 1 / Issue 1 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 81-96
- Print publication:
- June 2008
-
- Article
- Export citation
ULTIMATE TRUTH VIS-À-VIS STABLE TRUTH
-
- Journal:
- The Review of Symbolic Logic / Volume 1 / Issue 1 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 126-142
- Print publication:
- June 2008
-
- Article
- Export citation
A DECISION PROCEDURE FOR PROBABILITY CALCULUS WITH APPLICATIONS
-
- Journal:
- The Review of Symbolic Logic / Volume 1 / Issue 1 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 111-125
- Print publication:
- June 2008
-
- Article
- Export citation
A CUT-FREE SIMPLE SEQUENT CALCULUS FOR MODAL LOGIC S5
-
- Journal:
- The Review of Symbolic Logic / Volume 1 / Issue 1 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 3-15
- Print publication:
- June 2008
-
- Article
- Export citation
THE REVIEW OF SYMBOLIC LOGIC
-
- Journal:
- The Review of Symbolic Logic / Volume 1 / Issue 1 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 1-2
- Print publication:
- June 2008
-
- Article
- Export citation
TRUTH-FUNCTIONALITY
-
- Journal:
- The Review of Symbolic Logic / Volume 1 / Issue 1 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 64-72
- Print publication:
- June 2008
-
- Article
- Export citation
RECOGNIZING STRONG RANDOM REALS
-
- Journal:
- The Review of Symbolic Logic / Volume 1 / Issue 1 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 56-63
- Print publication:
- June 2008
-
- Article
- Export citation
THE CLOSING OF THE MIND: HOW THE PARTICULAR QUANTIFIER BECAME EXISTENTIALLY LOADED BEHIND OUR BACKS
-
- Journal:
- The Review of Symbolic Logic / Volume 1 / Issue 1 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 42-55
- Print publication:
- June 2008
-
- Article
- Export citation
Fully adaptive multiresolution schemes forstrongly degenerate parabolic equations in one space dimension
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 42 / Issue 4 / July 2008
- Published online by Cambridge University Press:
- 27 May 2008, pp. 535-563
- Print publication:
- July 2008
-
- Article
- Export citation
Approximation of solutions of Hamilton-Jacobi equationson the Heisenberg group
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 42 / Issue 4 / July 2008
- Published online by Cambridge University Press:
- 27 May 2008, pp. 565-591
- Print publication:
- July 2008
-
- Article
- Export citation
L 2 stability analysis of the central discontinuous Galerkin methodand a comparison between the central and regulardiscontinuous Galerkin methods
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 42 / Issue 4 / July 2008
- Published online by Cambridge University Press:
- 27 May 2008, pp. 593-607
- Print publication:
- July 2008
-
- Article
- Export citation
Optimal Poiseuille flow in a finite elastic dyadic tree
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 42 / Issue 4 / July 2008
- Published online by Cambridge University Press:
- 27 May 2008, pp. 507-533
- Print publication:
- July 2008
-
- Article
- Export citation
Interior-point methods for optimization
-
- Journal:
- Acta Numerica / Volume 17 / May 2008
- Published online by Cambridge University Press:
- 25 April 2008, pp. 191-234
-
- Article
- Export citation
Asymptotic and numerical homogenization
-
- Journal:
- Acta Numerica / Volume 17 / May 2008
- Published online by Cambridge University Press:
- 25 April 2008, pp. 147-190
-
- Article
- Export citation
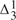 -
-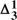 -comprehension axiom scheme) is insufficient. We briefly consider his claim to have produced a ‘revenge-immune’ solution to the semantic paradoxes by introducing this conditional. We remark that the notion of a ‘determinately true’ operator can be introduced in other settings.
-comprehension axiom scheme) is insufficient. We briefly consider his claim to have produced a ‘revenge-immune’ solution to the semantic paradoxes by introducing this conditional. We remark that the notion of a ‘determinately true’ operator can be introduced in other settings.