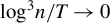Refine search
Actions for selected content:
52383 results in Statistics and Probability
Copyright page
-
- Book:
- Statistics for the Social Sciences
- Published online:
- 24 December 2020
- Print publication:
- 17 December 2020, pp iv-iv
-
- Chapter
- Export citation
ESTIMATION OF THE KRONECKER COVARIANCE MODEL BY QUADRATIC FORM
-
- Journal:
- Econometric Theory / Volume 38 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 17 December 2020, pp. 1014-1067
-
- Article
- Export citation
Dedication
-
- Book:
- Statistics for the Social Sciences
- Published online:
- 24 December 2020
- Print publication:
- 17 December 2020, pp v-vi
-
- Chapter
- Export citation
Acknowledgements
-
- Book:
- Statistics for the Social Sciences
- Published online:
- 24 December 2020
- Print publication:
- 17 December 2020, pp xiv-xv
-
- Chapter
- Export citation
13 - Regression
-
- Book:
- Statistics for the Social Sciences
- Published online:
- 24 December 2020
- Print publication:
- 17 December 2020, pp 375-409
-
- Chapter
- Export citation
References
-
- Book:
- Statistics for the Social Sciences
- Published online:
- 24 December 2020
- Print publication:
- 17 December 2020, pp 557-575
-
- Chapter
- Export citation
Appendix A2 - t-Table
-
- Book:
- Statistics for the Social Sciences
- Published online:
- 24 December 2020
- Print publication:
- 17 December 2020, pp 507-509
-
- Chapter
- Export citation
7 - Null Hypothesis Statistical Significance Testing and z-Tests
-
- Book:
- Statistics for the Social Sciences
- Published online:
- 24 December 2020
- Print publication:
- 17 December 2020, pp 152-182
-
- Chapter
- Export citation
Acknowledgements
-
- Book:
- Thinking Probabilistically
- Published online:
- 15 December 2020
- Print publication:
- 17 December 2020, pp viii-viii
-
- Chapter
- Export citation
Author Index
-
- Book:
- Statistics for the Social Sciences
- Published online:
- 24 December 2020
- Print publication:
- 17 December 2020, pp 576-579
-
- Chapter
- Export citation
Formula Guide
-
- Book:
- Statistics for the Social Sciences
- Published online:
- 24 December 2020
- Print publication:
- 17 December 2020, pp 537-541
-
- Chapter
- Export citation
11 - Analysis of Variance
-
- Book:
- Statistics for the Social Sciences
- Published online:
- 24 December 2020
- Print publication:
- 17 December 2020, pp 282-333
-
- Chapter
- Export citation
Appendix D - Review of Newtonian Mechanics, Basic Statistical Mechanics, and Hessians
-
- Book:
- Thinking Probabilistically
- Published online:
- 15 December 2020
- Print publication:
- 17 December 2020, pp 217-219
-
- Chapter
- Export citation
6 - Probability and the Central Limit Theorem
-
- Book:
- Statistics for the Social Sciences
- Published online:
- 24 December 2020
- Print publication:
- 17 December 2020, pp 128-151
-
- Chapter
- Export citation
Index
-
- Book:
- Thinking Probabilistically
- Published online:
- 15 December 2020
- Print publication:
- 17 December 2020, pp 232-234
-
- Chapter
- Export citation
Appendix A6 - χ2-Table
-
- Book:
- Statistics for the Social Sciences
- Published online:
- 24 December 2020
- Print publication:
- 17 December 2020, pp 519-520
-
- Chapter
- Export citation
Appendix C - Contour Integration and Fourier Transform Refresher
-
- Book:
- Thinking Probabilistically
- Published online:
- 15 December 2020
- Print publication:
- 17 December 2020, pp 214-216
-
- Chapter
- Export citation
3 - Models of Central Tendency and Variability
-
- Book:
- Statistics for the Social Sciences
- Published online:
- 24 December 2020
- Print publication:
- 17 December 2020, pp 36-61
-
- Chapter
- Export citation
12 - Correlation
-
- Book:
- Statistics for the Social Sciences
- Published online:
- 24 December 2020
- Print publication:
- 17 December 2020, pp 334-374
-
- Chapter
- Export citation
4 - Escape Over a Barrier
-
- Book:
- Thinking Probabilistically
- Published online:
- 15 December 2020
- Print publication:
- 17 December 2020, pp 67-80
-
- Chapter
- Export citation