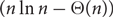Refine search
Actions for selected content:
52383 results in Statistics and Probability

Statistics for the Social Sciences
- A General Linear Model Approach
-
- Published online:
- 24 December 2020
- Print publication:
- 17 December 2020
-
- Textbook
- Export citation
Roughness-induced vehicle energy dissipation from crowdsourced smartphone measurements through random vibration theory
-
- Journal:
- Data-Centric Engineering / Volume 1 / 2020
- Published online by Cambridge University Press:
- 23 December 2020, e16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COPULA REPRESENTATIONS FOR THE SUM OF DEPENDENT RISKS: MODELS AND COMPARISONS
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 36 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 23 December 2020, pp. 320-340
-
- Article
- Export citation
How useful are survey data for analyzing immigration policy?
-
- Journal:
- Data & Policy / Volume 2 / 2020
- Published online by Cambridge University Press:
- 23 December 2020, e19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A meta-analysis of the association between obesity and COVID-19
-
- Journal:
- Epidemiology & Infection / Volume 149 / 2021
- Published online by Cambridge University Press:
- 22 December 2020, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Trusts, co-ops, and crowd workers: Could we include crowd data workers as stakeholders in data trust design?
-
- Journal:
- Data & Policy / Volume 2 / 2020
- Published online by Cambridge University Press:
- 22 December 2020, e20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CLOUD STORAGE FACILITY AS A FLUID QUEUE CONTROLLED BY MARKOVIAN QUEUE
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 36 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 21 December 2020, pp. 237-253
-
- Article
- Export citation
Cycle partitions of regular graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 4 / July 2021
- Published online by Cambridge University Press:
- 18 December 2020, pp. 526-549
-
- Article
- Export citation
2 - Levels of Data
-
- Book:
- Statistics for the Social Sciences
- Published online:
- 24 December 2020
- Print publication:
- 17 December 2020, pp 22-35
-
- Chapter
- Export citation
4 - Visual Models
-
- Book:
- Statistics for the Social Sciences
- Published online:
- 24 December 2020
- Print publication:
- 17 December 2020, pp 62-103
-
- Chapter
- Export citation
3 - Langevin and Fokker–Planck Equations and Their Applications
-
- Book:
- Thinking Probabilistically
- Published online:
- 15 December 2020
- Print publication:
- 17 December 2020, pp 39-66
-
- Chapter
- Export citation
Examples
-
- Book:
- Statistics for the Social Sciences
- Published online:
- 24 December 2020
- Print publication:
- 17 December 2020, pp xvi-xx
-
- Chapter
- Export citation
8 - Random Matrix Theory
-
- Book:
- Thinking Probabilistically
- Published online:
- 15 December 2020
- Print publication:
- 17 December 2020, pp 145-183
-
- Chapter
- Export citation
14 - Chi-Squared Test
-
- Book:
- Statistics for the Social Sciences
- Published online:
- 24 December 2020
- Print publication:
- 17 December 2020, pp 410-455
-
- Chapter
- Export citation
Contents
-
- Book:
- Thinking Probabilistically
- Published online:
- 15 December 2020
- Print publication:
- 17 December 2020, pp v-vii
-
- Chapter
- Export citation
The effect of hemicylindrical disruptors on the cell free layer thickness in animal blood flows inside microchannels
-
- Journal:
- Experimental Results / Volume 1 / 2020
- Published online by Cambridge University Press:
- 17 December 2020, e55
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Counting Hamilton cycles in Dirac hypergraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 4 / July 2021
- Published online by Cambridge University Press:
- 17 December 2020, pp. 631-653
-
- Article
- Export citation
1 - Statistics and Models
-
- Book:
- Statistics for the Social Sciences
- Published online:
- 24 December 2020
- Print publication:
- 17 December 2020, pp 1-21
-
- Chapter
- Export citation
Contents
-
- Book:
- Statistics for the Social Sciences
- Published online:
- 24 December 2020
- Print publication:
- 17 December 2020, pp vii-viii
-
- Chapter
- Export citation
Context-specific volume–delay curves by combining crowd-sourced traffic data with automated traffic counters: A case study for London
-
- Journal:
- Data-Centric Engineering / Volume 1 / 2020
- Published online by Cambridge University Press:
- 17 December 2020, e18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation