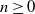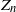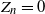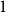Refine search
Actions for selected content:
52315 results in Statistics and Probability
Asymptotics of the allele frequency spectrum and the number of alleles
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 22 November 2024, pp. 516-540
- Print publication:
- June 2025
-
- Article
- Export citation
Should we communicate with the dead to assuage our grief? An Ubuntu perspective on using griefbots
- Part of
-
- Journal:
- Data & Policy / Volume 6 / 2024
- Published online by Cambridge University Press:
- 22 November 2024, e55
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
5 - Experimental Designs and Typologies
- from Part I - The Philosophy and Methodology of Experimentation in Sociology
-
- Book:
- Experimental Sociology
- Published online:
- 23 November 2024
- Print publication:
- 21 November 2024, pp 52-66
-
- Chapter
- Export citation
6 - Some Extensions and Applications of Martingale Theory
-
- Book:
- Probability Theory, An Analytic View
- Published online:
- 07 November 2024
- Print publication:
- 21 November 2024, pp 200-234
-
- Chapter
- Export citation
Appendix B - Advanced Topics in Classification Metrics
- from Appendices
-
- Book:
- Machine Learning Evaluation
- Published online:
- 07 November 2024
- Print publication:
- 21 November 2024, pp 373-386
-
- Chapter
- Export citation
Boxes
-
- Book:
- Introduction to Catastrophe Risk Modelling
- Published online:
- 08 November 2024
- Print publication:
- 21 November 2024, pp xvi-xvi
-
- Chapter
- Export citation
Contents
-
- Book:
- Machine Learning Evaluation
- Published online:
- 07 November 2024
- Print publication:
- 21 November 2024, pp vii-x
-
- Chapter
- Export citation
Tables
-
- Book:
- Introduction to Catastrophe Risk Modelling
- Published online:
- 08 November 2024
- Print publication:
- 21 November 2024, pp xv-xv
-
- Chapter
- Export citation
Contents
-
- Book:
- Probability Theory, An Analytic View
- Published online:
- 07 November 2024
- Print publication:
- 21 November 2024, pp vii-xii
-
- Chapter
- Export citation
Contents
-
- Book:
- Introduction to Catastrophe Risk Modelling
- Published online:
- 08 November 2024
- Print publication:
- 21 November 2024, pp vii-x
-
- Chapter
- Export citation
References
-
- Book:
- Introduction to Catastrophe Risk Modelling
- Published online:
- 08 November 2024
- Print publication:
- 21 November 2024, pp 276-330
-
- Chapter
- Export citation
Regeneration of branching processes with immigration in varying environments
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 21 November 2024, pp. 422-444
- Print publication:
- March 2025
-
- Article
- Export citation
On the smallest gap in a sequence with Poisson pair correlations
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 21 November 2024, pp. 283-297
-
- Article
- Export citation
7 - Continuous Parameter Martingales
-
- Book:
- Probability Theory, An Analytic View
- Published online:
- 07 November 2024
- Print publication:
- 21 November 2024, pp 235-263
-
- Chapter
- Export citation
12 - Conclusion
- from Part IV - Evaluation from a Practical Perspective
-
- Book:
- Machine Learning Evaluation
- Published online:
- 07 November 2024
- Print publication:
- 21 November 2024, pp 342-358
-
- Chapter
- Export citation
12 - Ethics and Deception
- from Part III - Methodological Challenges of Experimentation in Sociology
-
- Book:
- Experimental Sociology
- Published online:
- 23 November 2024
- Print publication:
- 21 November 2024, pp 144-153
-
- Chapter
- Export citation
3 - Infinitely Divisible Laws
-
- Book:
- Probability Theory, An Analytic View
- Published online:
- 07 November 2024
- Print publication:
- 21 November 2024, pp 101-130
-
- Chapter
- Export citation
Appendices
-
- Book:
- Machine Learning Evaluation
- Published online:
- 07 November 2024
- Print publication:
- 21 November 2024, pp 359-360
-
- Chapter
- Export citation
3 - Probabilistic Risk Assessment
- from Part I - Basics of CAT Modelling
-
- Book:
- Introduction to Catastrophe Risk Modelling
- Published online:
- 08 November 2024
- Print publication:
- 21 November 2024, pp 118-158
-
- Chapter
- Export citation
Cyber risk within capital models
-
- Journal:
- British Actuarial Journal / Volume 29 / 2024
- Published online by Cambridge University Press:
- 21 November 2024, e16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation