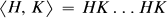Contents
Research Article
Explicit Formulas for the Coefficients of α-Convex Functions, α ≧ 0
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 769-783
-
- Article
-
- You have access
- Export citation
The Multiplicative Groups of Quasifields
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 784-793
-
- Article
-
- You have access
- Export citation
The Empty Sphere
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 794-824
-
- Article
-
- You have access
- Export citation
On The Factorization of Partial Differential Equations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 825-834
-
- Article
-
- You have access
- Export citation
A Descent Theorem for Hermitian K-Theory
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 835-847
-
- Article
-
- You have access
- Export citation
Simple Type III Self-Injective Rings and Rings of Column-Finite Matrices
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 848-879
-
- Article
-
- You have access
- Export citation
Three Test Problems for Quasisimilarity
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 880-892
-
- Article
-
- You have access
- Export citation
Classification Theory and Stationary Logic
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 893-907
-
- Article
-
- You have access
- Export citation
Compact 16-Dimensional Projective Planes with Large Collineation Groups. IV
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 908-919
-
- Article
-
- You have access
- Export citation
Character Correspondences and π-Special Characters in π-Separable Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 920-937
-
- Article
-
- You have access
- Export citation
Decomposable Free Loop Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 938-955
-
- Article
-
- You have access
- Export citation
On Elliptically Embedded Subgroups of Soluble Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 956-968
-
- Article
-
- You have access
- Export citation
Uniqueness of Free Actions on S 3 Respecting a Knot
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 969-982
-
- Article
-
- You have access
- Export citation
Explicit Formulas for the Associated Jacobi Polynomials and Some Applications
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 983-1000
-
- Article
-
- You have access
- Export citation
Divisible Semiplanes, Arcs, and Relative Difference Sets
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1001-1024
-
- Article
-
- You have access
- Export citation



 of
of 




 generate the stable one-stem. Then there are weak equivalences of spectra
generate the stable one-stem. Then there are weak equivalences of spectra
 and
and
 and
and  , are said to be quasisimilar if there exist bounded operators
, are said to be quasisimilar if there exist bounded operators  and
and  with densely defined inverses, satisfying the relations
with densely defined inverses, satisfying the relations 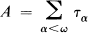
 be a topological projective plane with compact point set
be a topological projective plane with compact point set