We characterize positive links in terms of strong quasipositivity, homogeneity, and thevalue of Rasmussen and Beliakova-Wehrli's $s$ -invariant. We also study almost positive links, and inparticular, determine the $s$ -invariants of almost positive links. This result suggests that all almostpositive links might be strongly quasipositive. On the other hand, it implies that almost positivelinks are never homogeneous links.

In this paper we introduce Hardy-Lorentz spaces with variable exponents associated withdilations in ${{\mathbb{R}}^{n}}$ . We establish maximal characterizations and atomic decompositions for our variableexponent anisotropic Hardy-Lorentz spaces.

A current research theme is to compare symbolic powers of an ideal $I$ with the regular powers of $I$ . In this paper, we focus on the case where $I\,=\,{{I}_{X}}$ is an ideal defining an almost complete intersection (ACI) set of points $X$ in ${{\mathbb{P}}^{1}}\,\times \,{{\mathbb{P}}^{1}}$ . In particular, we describe a minimal free bigraded resolution of a non-arithmetically Cohen-Macaulay (also non-homogeneous) set $Z$ of fat points whose support is an ACI, generalizing an earlier result of Cooper et al. for homogeneous sets of triple points. We call $Z$ a fat ACI. We also show that its symbolic and ordinary powers are equal, i.e, $I_{Z}^{\left( m \right)}\,=\,I_{Z}^{m}$ for any $m\,\ge \,1$ .

In this article, we study complete surfaces $\sum $ , isometrically immersed in the product spaces ${{\mathbb{H}}^{2}}\,\times \,\mathbb{R}$ or ${{\mathbb{S}}^{2\,}}\times \,\mathbb{R}$ having positive extrinsic curvature ${{K}_{e}}$ . Let ${{K}_{i}}$ denote the intrinsic curvature of $\sum $ . Assume that the equation $a{{K}_{i\,}}\,+\,b{{K}_{e\,}}\,=\,c$ holds for some real constants $a\,\ne \,0$ , $b\,>\,0$ , and $c$ . The main result of this article states that when such a surface is a topological sphere, it is rotational.

An asymptotically orthonormal sequence is a sequence that is nearly orthonormal in the sense that it satisfies the Parseval equality up to two constants close to one. In this paper, we explore such sequences formed by normalized reproducing kernels for model spaces and de Branges–Rovnyak spaces.

We investigate when a computable automorphism of a computable field can be effectively extended to a computable automorphism of its (computable) algebraic closure. We then apply our results and techniques to study effective embeddings of computable difference fields into computable difference closed fields.

We prove that the extremal sequences for the Bellman function of the dyadic maximal operator behave approximately as eigenfunctions of this operator for a specific eigenvalue. We use this result to prove the analogous one with respect to the Hardy operator.

Following up on previous work, we prove a number of results for 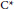${{\text{C}}^{*}}$ -algebras with the weak ideal property or topological dimension zero, and some results for 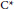${{\text{C}}^{*}}$ -algebras with related properties. Some of the more important results include the following:

• The weak ideal property implies topological dimension zero.

• For a separable 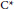${{\text{C}}^{*}}$ -algebra $A$ , topological dimension zero is equivalent to 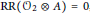$\text{RR}\left( {{\mathcal{O}}_{2}}\otimes A \right)=0$ , to 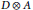$D\,\otimes \,A$ having the ideal property for some (or any) Kirchberg algebra $D$ , and to $A$ being residually hereditarily in the class of all 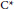${{\text{C}}^{*}}$ -algebras $B$ such that 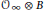${{\mathcal{O}}_{\infty }}\otimes B$ contains a nonzero projection.

• Extending the known result for 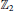${{\mathbb{Z}}_{2}}$ , the classes of 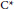${{\text{C}}^{*}}$ -algebras with residual 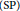$\left( \text{SP} \right)$ , which are residuallyhereditarily (properly) infinite, or which are purely infinite and have the ideal property, areclosed under crossed products by arbitrary actions of abelian 2-groups.

• If $A$ and $B$ are separable, one of them is exact, $A$ has the ideal property, and $B$ has the weak idealproperty, then 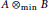$A\,{{\otimes }_{\min }}\,B$ has the weak ideal property.

• If 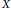$X$ is a totally disconnected locally compact Hausdorff space and $A$ is a 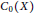${{C}_{0}}\left( X \right)$ -algebra all of whose fibers have one of the weak ideal property, topological dimension zero, residual 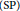$\left( \text{SP} \right)$ , or the combination of pure infiniteness and the ideal property, then $A$ also has the corresponding property (for topological dimension zero, provided $A$ is separable).

• Topological dimension zero, the weak ideal property, and the ideal property are all equivalent for a substantial class of separable 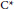${{\text{C}}^{*}}$ -algebras, including all separable locally 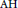$\text{AH}$ algebras.

• The weak ideal property does not imply the ideal property for separable $Z$ -stable 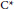${{\text{C}}^{*}}$ -algebras.

We give other related results, as well as counterexamples to several other statements one might conjecture.

We describe the general form of surjective maps on the cone of all positive operators that preserve order and spectrum. The result is optimal as shown by counterexamples. As an easy consequence, we characterize surjective order and spectrum preserving maps on the set of all self-adjoint operators.