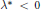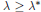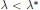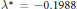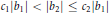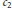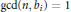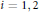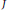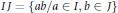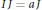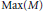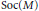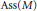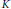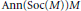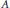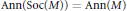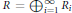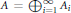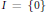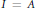Contents
Research Article
Quantum Multiple Construction of Subfactors
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 321-333
-
- Article
-
- You have access
- Export citation
Value Distribution of the Riemann Zeta Function
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 334-336
-
- Article
-
- You have access
- Export citation
Differences between Perfect Powers
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 337-347
-
- Article
-
- You have access
- Export citation
The Reconstruction Property in Banach Spaces and a Perturbation Theorem
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 348-358
-
- Article
-
- You have access
- Export citation
Real Hypersurfaces in Complex Space Forms with Reeb Flow Symmetric Structure Jacobi Operator
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 359-371
-
- Article
-
- You have access
- Export citation
Picard's Iterations for Integral Equations of Mixed Hammerstein Type
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 372-377
-
- Article
-
- You have access
- Export citation
Cyclic Vectors in Some Weighted Lp Spaces of Entire Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 378-385
-
- Article
-
- You have access
- Export citation
Positive Solutions of the Falkner–Skan Equation Arising in the Boundary Layer Theory
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 386-398
-
- Article
-
- You have access
- Export citation
Linear Equations with Small Prime and Almost Prime Solutions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 399-405
-
- Article
-
- You have access
- Export citation
Condensed and Strongly Condensed Domains
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 406-412
-
- Article
-
- You have access
- Export citation
Big Ramsey Degrees and Divisibility in Classes of Ultrametric Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 413-423
-
- Article
-
- You have access
- Export citation
Noncommutative Symmetric Bessel Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 424-438
-
- Article
-
- You have access
- Export citation
On the Maximal Spectrum of Semiprimitive Multiplication Modules
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 439-447
-
- Article
-
- You have access
- Export citation
Stability of Biharmonic Legendrian Submanifolds in Sasakian Space Forms
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 448-459
-
- Article
-
- You have access
- Export citation
On Primitive Ideals in Graded Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 460-466
-
- Article
-
- You have access
- Export citation
Coupled Vortex Equations on Complete Kähler Manifolds
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 467-480
-
- Article
-
- You have access
- Export citation