In a planar smoothly bounded domain 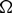 $\Omega$, we consider the model for oncolytic virotherapy given by
$\Omega$, we consider the model for oncolytic virotherapy given by 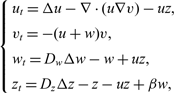 $$\left\{ \begin{array}{l} u_t = \Delta u - \nabla \cdot (u\nabla v) - uz, \\[1mm] v_t = - (u+w)v, \\[1mm] w_t = d_w \Delta w - w + uz, \\[1mm] z_t = d_z \Delta z - z - uz + \beta w, \end{array} \right.$$
$$\left\{ \begin{array}{l} u_t = \Delta u - \nabla \cdot (u\nabla v) - uz, \\[1mm] v_t = - (u+w)v, \\[1mm] w_t = d_w \Delta w - w + uz, \\[1mm] z_t = d_z \Delta z - z - uz + \beta w, \end{array} \right.$$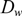 $ D_w $,
$ D_w $, 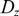 $ D_z $ and
$ D_z $ and 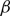 $\beta$. It is firstly shown that whenever
$\beta$. It is firstly shown that whenever 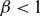 $\beta \lt 1$, for any choice of
$\beta \lt 1$, for any choice of 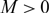 $M \gt 0$, one can find initial data such that the solution of an associated no-flux initial-boundary value problem, well known to exist globally actually for any choice of
$M \gt 0$, one can find initial data such that the solution of an associated no-flux initial-boundary value problem, well known to exist globally actually for any choice of 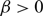 $\beta \gt 0$, satisfies
$\beta \gt 0$, satisfies 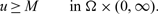 $$u\ge M \qquad \mbox{in } \Omega\times (0,\infty).$$
$$u\ge M \qquad \mbox{in } \Omega\times (0,\infty).$$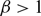 $\beta \gt 1$, however, then for arbitrary initial data the corresponding is seen to have the property that
$\beta \gt 1$, however, then for arbitrary initial data the corresponding is seen to have the property that 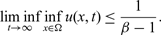 $$\liminf_{t\to\infty} \inf_{x\in\Omega} u(x,t)\le \frac{1}{\beta-1}.$$
$$\liminf_{t\to\infty} \inf_{x\in\Omega} u(x,t)\le \frac{1}{\beta-1}.$$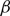 $\beta$ plays the role of a critical virus replication rate with regard to efficiency of the considered virotherapy, with corresponding threshold value given by
$\beta$ plays the role of a critical virus replication rate with regard to efficiency of the considered virotherapy, with corresponding threshold value given by 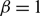 $\beta = 1$.
$\beta = 1$.