Contents
Research Article
Co-H-Structures on Moore Spaces of Type (G, 2)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 673-686
-
- Article
-
- You have access
- Export citation
Exact Inequalities for the Norms of Factors of Polynomials
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 687-698
-
- Article
-
- You have access
- Export citation
Conjugacy Classes of Maximal Tori in Simple Real Algebraic Groups and Applications
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 699-717
-
- Article
-
- You have access
- Export citation
Cocharacters, Codimensions and Hilbert Series of the Polynomial Identities for 2 × 2 Matrices with Involution
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 718-733
-
- Article
-
- You have access
- Export citation
Homomorphisms on Function Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 734-745
-
- Article
-
- You have access
- Export citation
A Convexity Theorem for Boundariesof Ordered Symmetric Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 746-757
-
- Article
-
- You have access
- Export citation
Separating Points of βℕ By Minimal Flows
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 758-771
-
- Article
-
- You have access
- Export citation
Formulas for Brown-Peterson Operations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 772-792
-
- Article
-
- You have access
- Export citation
Simplicity Of Reduced Amalgamated Products of C*-Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 793-807
-
- Article
-
- You have access
- Export citation
The Extensions of an Invariant Mean and the Set LIM ∽ TLIM
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 808-817
-
- Article
-
- You have access
- Export citation
Reduction of Exponential Rank in Direct Limits of C*-Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 818-853
-
- Article
-
- You have access
- Export citation
Products of Decomposable Positive Operators
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 854-871
-
- Article
-
- You have access
- Export citation
Weakly Purely Finitely Additive Measures
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 872-885
-
- Article
-
- You have access
- Export citation
Extra-Special Groups of Order 32 as Galois Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 886-896
-
- Article
-
- You have access
- Export citation
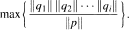
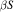 of a topological semigroup
of a topological semigroup  , and the compactification is
, and the compactification is 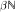 . Included is the statement that some set
. Included is the statement that some set 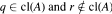 .
.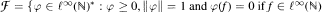 with
with 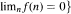 . If
. If 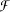 into the set of all extensions of m to left invariant means on
into the set of all extensions of m to left invariant means on 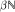 is a very big set. We also embed
is a very big set. We also embed 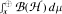 with
with  separable and infinite dimensional. We generalize a theorem of Wu (1988) and characterize those decomposable operators which are products of non-negative decomposable operators. We do this by first showing that various results on operator ranges may be generalized to “measurable fields of operator ranges”.
separable and infinite dimensional. We generalize a theorem of Wu (1988) and characterize those decomposable operators which are products of non-negative decomposable operators. We do this by first showing that various results on operator ranges may be generalized to “measurable fields of operator ranges”.