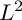 $L^{2}$ INTEGRALS WITH LEBESGUE MEASURABLE GAIN
$L^{2}$ INTEGRALS WITH LEBESGUE MEASURABLE GAIN
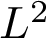 $L^{2}$
EXTENSION THEOREM AND A QUESTION OF OHSAWA
$L^{2}$
EXTENSION THEOREM AND A QUESTION OF OHSAWA