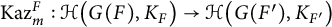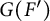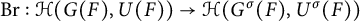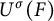Refine listing
Actions for selected content:
1419635 results in Open Access
Human brain evolution in a Malthusian economy
-
- Journal:
- Macroeconomic Dynamics / Volume 29 / 2025
- Published online by Cambridge University Press:
- 22 November 2024, e59
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Compatibility of Kazhdan and Brauer homomorphism
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 22 November 2024, pp. 19-43
- Print publication:
- March 2025
-
- Article
- Export citation
Continuing the momentum of developmental psychopathology: Lessons learned from the seminal contributions of Dante Cicchetti
-
- Journal:
- Development and Psychopathology / Volume 36 / Issue 5 / December 2024
- Published online by Cambridge University Press:
- 22 November 2024, pp. 2051-2055
-
- Article
-
- You have access
- HTML
- Export citation
Butyrate attenuates high-fat diet-induced glomerulopathy through GPR43-Sirt3 pathway
-
- Journal:
- British Journal of Nutrition / Volume 133 / Issue 1 / 14 January 2025
- Published online by Cambridge University Press:
- 22 November 2024, pp. 1-10
- Print publication:
- 14 January 2025
-
- Article
- Export citation
Asking the right questions on Rayleigh–Bénard turbulence
-
- Journal:
- Journal of Fluid Mechanics / Volume 1000 / 10 December 2024
- Published online by Cambridge University Press:
- 22 November 2024, F3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Anatomic and non-anatomic substrates in infants with two ventricles undergoing aortic arch repair
-
- Journal:
- Cardiology in the Young / Volume 35 / Issue 2 / February 2025
- Published online by Cambridge University Press:
- 22 November 2024, pp. 253-260
-
- Article
- Export citation
Fence of saddle solutions of the Allen–Cahn equation in the plane
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 22 November 2024, pp. 1-42
-
- Article
- Export citation
Log at first sight
-
- Journal:
- Journal of Fluid Mechanics / Volume 1000 / 10 December 2024
- Published online by Cambridge University Press:
- 22 November 2024, F6
-
- Article
-
- You have access
- HTML
- Export citation
Ultra-fast imaging reveals
-
- Journal:
- Journal of Fluid Mechanics / Volume 1000 / 10 December 2024
- Published online by Cambridge University Press:
- 22 November 2024, F8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Shipping the Color Line: Migration and Transport Policy in the British Empire, 1943–51
-
- Journal:
- Journal of British Studies / Volume 63 / Issue 4 / October 2024
- Published online by Cambridge University Press:
- 22 November 2024, pp. 810-835
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Picture-Reading the Complexities of Transgender Experience
-
- Journal:
- Canadian Journal of Philosophy / Volume 53 / Issue 7-8 / October 2023
- Published online by Cambridge University Press:
- 22 November 2024, pp. 600-609
-
- Article
- Export citation
JPH volume 36 issue 4 Cover and Front matter
-
- Journal:
- Journal of Policy History / Volume 36 / Issue 4 / October 2024
- Published online by Cambridge University Press:
- 22 November 2024, pp. f1-f4
-
- Article
-
- You have access
- Export citation
Elementary quantum recursion schemes that capture quantum polylogarithmic-time computability of quantum functions
-
- Journal:
- Mathematical Structures in Computer Science / Volume 34 / Issue 7 / August 2024
- Published online by Cambridge University Press:
- 22 November 2024, pp. 710-745
-
- Article
- Export citation
Contributors
-
- Journal:
- Ethics & International Affairs / Volume 38 / Issue 2 / Summer 2024
- Published online by Cambridge University Press:
- 22 November 2024, pp. 135-136
-
- Article
- Export citation
Timed array architectures and integrated true-time delay elements for wideband millimeter-wave antenna arrays
-
- Journal:
- International Journal of Microwave and Wireless Technologies / Volume 17 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 22 November 2024, pp. 190-201
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptomatic Optic Disc Oedema due to Haematologic Malignancy
-
- Journal:
- Canadian Journal of Neurological Sciences / Volume 52 / Issue 5 / September 2025
- Published online by Cambridge University Press:
- 22 November 2024, pp. 874-875
-
- Article
- Export citation
A criterion to detect a non-trivial homology of an invariant set of a flow in
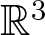 $\mathbb{R}^3$
$\mathbb{R}^3$
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 22 November 2024, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
IPG volume 36 issue 10 Front matter
-
- Journal:
- International Psychogeriatrics / Volume 36 / Issue 10 / October 2024
- Published online by Cambridge University Press:
- 22 November 2024, pp. f1-f3
-
- Article
-
- You have access
- Export citation
A dual-frequency measurement setup with fully integrated SiGe-based radar sensors for the size estimation of particulate matter
-
- Journal:
- International Journal of Microwave and Wireless Technologies / Volume 17 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 22 November 2024, pp. 365-372
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Adjusting to dementia as part of life: an actantial analysis of agency reconstruction following diagnosis of young onset dementia
-
- Journal:
- Ageing & Society / Volume 45 / Issue 10 / October 2025
- Published online by Cambridge University Press:
- 22 November 2024, pp. 1970-1996
- Print publication:
- October 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation