For $E \subset \mathbb {N}$, a subset $R \subset \mathbb {N}$ is E-intersective if for every $A \subset E$ having positive relative density, $R \cap (A - A) \neq \varnothing $. We say that R is chromatically E-intersective if for every finite partition $E=\bigcup _{i=1}^k E_i$, there exists i such that $R\cap (E_i-E_i)\neq \varnothing $. When $E=\mathbb {N}$, we recover the usual notions of intersectivity and chromatic intersectivity. We investigate to what extent the known intersectivity results hold in the relative setting when $E = \mathbb {P}$, the set of primes, or other sparse subsets of $\mathbb {N}$. Among other things, we prove the following: (1) the set of shifted Chen primes $\mathbb {P}_{\mathrm {Chen}} + 1$ is both intersective and $\mathbb {P}$-intersective; (2) there exists an intersective set that is not $\mathbb {P}$-intersective; (3) every $\mathbb {P}$-intersective set is intersective; (4) there exists a chromatically $\mathbb {P}$-intersective set which is not intersective (and therefore not $\mathbb {P}$-intersective).

We prove three results concerning the existence of Bohr sets in threefold sumsets. More precisely, letting G be a countable discrete abelian group and 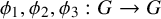$\phi _1, \phi _2, \phi _3: G \to G$ be commuting endomorphisms whose images have finite indices, we show that

1. (1) If 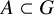$A \subset G$ has positive upper Banach density and 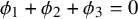$\phi _1 + \phi _2 + \phi _3 = 0$, then 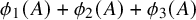$\phi _1(A) + \phi _2(A) + \phi _3(A)$ contains a Bohr set. This generalizes a theorem of Bergelson and Ruzsa in 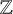$\mathbb {Z}$ and a recent result of the first author.

2. (2) For any partition 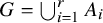$G = \bigcup _{i=1}^r A_i$, there exists an 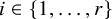$i \in \{1, \ldots , r\}$ such that 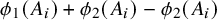$\phi _1(A_i) + \phi _2(A_i) - \phi _2(A_i)$ contains a Bohr set. This generalizes a result of the second and third authors from 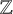$\mathbb {Z}$ to countable abelian groups.

3. (3) If 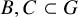$B, C \subset G$ have positive upper Banach density and 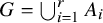$G = \bigcup _{i=1}^r A_i$ is a partition, 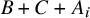$B + C + A_i$ contains a Bohr set for some 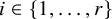$i \in \{1, \ldots , r\}$. This is a strengthening of a theorem of Bergelson, Furstenberg and Weiss.

All results are quantitative in the sense that the radius and rank of the Bohr set obtained depends only on the indices 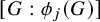$[G:\phi _j(G)]$, the upper Banach density of A (in (1)), or the number of sets in the given partition (in (2) and (3)).

We observed a bright H II complex, Hubble V in NGC 6822, using the high-resolution near-infrared spectrograph IGRINS (R = 45,000) attached on the 2.7 m telescope at the McDonald Observatory. We carried out a spectral mapping over a 15″ × 18″ region in the H and K bands using a slit-scanning technique. The emission lines Brγ and He i from ionized regions as well as molecular hydrogen lines from photo-dissociation regions (PDRs), were detected. We show three-dimensional maps of the emission lines and discuss the possibility of an expanding hot bubble structure within which many ionized components are around the central stellar cluster.