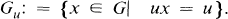The so-called Burnside–Dixon–Schneider (BDS) method, currently used as the default method of computing character tables in GAP for groups which are not solvable, is often inefficient in dealing with groups with large centres. If $G$ is a finite group with centre $Z$ and $\lambda $ a linear character of $Z$ , then we describe a method of computing the set $\mathrm{Irr} (G, \lambda )$ of irreducible characters $\chi $ of $G$ whose restriction ${\chi }_{Z} $ is a multiple of $\lambda $ . This modification of the BDS method involves only $\vert \mathrm{Irr} (G, \lambda )\vert $ conjugacy classes of $G$ and so is relatively fast. A generalization of the method can be applied to computation of small sets of characters of groups with a solvable normal subgroup.

Supplementary materials are available with this article.

The natural character π of a finite transitive permutation group G has the form 1G + θ where θ is a character which affords a rational representation of G. We call G a QI-group if this representation is irreducible over ℚ. Every 2-transitive group is a QI-group, but the latter class of groups is larger. It is shown that every QI-group is ¾-transitive and primitive, and that it is either almost simple or of affine type. QI-groups of affine type are completely determined relative to the 2-transitive affine groups, and partial information is obtained about the socles of simply transitive almost simple QI-groups. The only known simply transitive almost simple QI-groups are of degree 2k−1(2k − 1) with 2k − 1 prime and socle isomorphic to PSL(2, 2k).

Let $G$ be a finite group and $H$ be a subgroup. We say that $H$ is degree homogeneous if, for each $x\,\in \,\text{Irr}\left( G \right)$ , all the irreducible constituents of the restriction ${{x}_{H}}$ have the same degree. Subgroups which are either normal or abelian are obvious examples of degree homogeneous subgroups. Following a question by E.M. Zhmud’, we investigate general properties of such subgroups. It appears unlikely that degree homogeneous subgroups can be characterized entirely by abstract group properties, but we providemixed criteria (involving both group structure and character properties) which are both necessary and sufficient. For example, $H$ is degree homogeneous in $G$ if and only if the derived subgroup ${H}'$ is normal in $G$ and, for every pair $\alpha $ , $\beta $ of irreducible $G$ -conjugate characters of ${H}'$ , all irreducible constituents of ${{\alpha }^{H}}$ and ${{\beta }^{H}}$ have the same degree.

The set ℳ* of numbers which occur as Mahler measures of integer polynomials and the subset ℳ of Mahler measures of algebraic numbers (that is, of irreducible integer polynomials) are investigated. It is proved that every number α of degree d in ℳ* is the Mahler measure of a separable integer polynomial of degree at most with all its roots lying in the Galois closure F of ℚ(α), and every unit in ℳ is the Mahler measure of a unit in F of degree at most over ℚ This is used to show that some numbers considered earlier by Boyd are not Mahler measures. The set of numbers which occur as Mahler measures of both reciprocal and nonreciprocal algebraic numbers is also investigated. In particular, all cubic units in this set are described and it is shown that the smallest Pisot number is not the measure of a reciprocal number.

A process is described for enumerating the Cayley graphs isomorphic to a binary d-cube for small values of d. There are 4 Cayley graphs isomorphic to the 3-cube, 14 isomorphic to the 4-cube, 45 isomorphic to the 5-cube and 238 isomorphic to the 6-cube. A similar method may be used for any graph with a prime power number of vertices.

Let K:= Q(α) be an algebraic number field which is given by specifying the minimal polynomial f(X) for α over Q. We describe a procedure for finding the subfields L of K by constructing pairs (w(X), g(X)) of polynomials over Q such that L= Q(w(α)) and g(X) is the minimal polynomial for w(α). The construction uses local information obtained from the Frobenius-Chebotarev theorem about the Galois group Gal(f), and computations over p-adic extensions of Q.

Our object is to describe all of the-primitive permutation groups of degree less than 1000 together with some of their significant properties. We think that such a list is of interest in illustrating in concrete form the kinds of primitive groups which arise, in suggesting conjectures about primitive groups, and in settling small exceptional cases which often occur in proofs of theorems about permutation groups. The range that we consider is large enough to allow examples of most of the types of primitive group to appear. Earlier lists (of varying completeness and accuracy) of primitive groups of degree d have been published by: C. Jordan (1872) [21] for d ≤ 17, by W. Burnside (1897) [5] for d ≤ 8, by Manning (1929) [34–38] for d ≤ 15, by C. C. Sims (1970) [45] for d ≤ 20, and by B. A. Pogorelev (1980) [42] for d ≤ 50. Unpublished lists have also been prepared by C. C. Sims for d ≤ 50 and by Mizutani[41] for d ≤ 48. Using the classification of finite simple groups which was completed in 1981 we have been able to extend the list much further. Our task has been greatly simplified by the detailed information about many finite simple groups which is available in the Atlas of Finite Groups which we will refer to as the Atlas [8].

Let G be a subgroup of the general linear group GL(n, Q) over the rational field Q, and consider its action by right multiplication on the vector space Q n of n-tuples over Q. The present paper investigates the question of how we may constructively determine the orbits and stabilizers of this action for suitable classes of groups. We suppose that G is specified by a finite set {x 1, …, xr ) of generators, and investigate whether there exist algorithms to solve the two problems:

(Orbit Problem) Given u, v ∊ Q n , does there exist x ∊ G such that ux = v; if so, find such an element x as a word in x 1, …, xr and their inverses.

(Stabilizer Problem) Given u, v ∊ Q n , describe all words in x 1, …, xr and their inverses which lie in the stabilizer

Let A be a real n × n matrix and define the Hadamard ratio h(A) to be the absolute value of det A divided by the product of the Euclidean norms of the columns of A. It is shown that if A is a random variable whose distribution satisfies some simple symmetry properties then the random variable log h(A) has mean and variance . In particular, for each ε > 0, the probability that h(A) lies in the range tends to 1 as n tends to ∞.

Let K be a (commutative) field and n be a positive integer. Consider the K-algebra E = Mat (n, K) of all n X n matrices over K, and the corresponding general linear group GL(n, K). We shall define the set R of rigid mappings of E to consist of all a in GLK(E) which can be written in one of two possible forms: either x σ= axb for all x ϵ E or xσ = ax'b for all x ϵ E (where a and b are fixed elements of GL(n, K) and x’ denotes the transpose of x).

Our aim is to present some global results about the set of maximal abelian subgroups of the symmetric group Sn. We shall show that certain properties are true for “almost all” subgroups of this set in the sense that the proportion of subgroups which have these properties tends to 1 as n → ∞. In this context we consider the order and the number of orbits of a maximal abelian subgroup and the number of generators which the group requires.

Earlier results of this kind may be found in the papers [1; 2; 3; 4; 5]; the papers of Erdös and Turán deal with properties of the set of elements of Sn. The present work arose out of a conversation with Professor Turán who posed the general problem: given a specific class of subgroups (e.g., the abelian subgroups or the solvable subgroups) of Sn , what kind of properties hold for almost all subgroups of the class?

Let G be a group. The Fitting subgroup F(G) of G is defined to be the set union of all normal nilpotent subgroups of G. Since the product of two normal nilpotent subgroups is again a normal nilpotent subgroup (see [10] p. 238), F(G) is the unique maximal normal, locally nilpotent sungroup of G. In particular, is G is finite, then F(G) is the unique maximal normal nilpotent subgroup of G. If G is a notrivial solvable group, then clearly F(G) ≠1.