 $M_{p}$-GROUPS AND BRAUER CHARACTER DEGREES
$M_{p}$-GROUPS AND BRAUER CHARACTER DEGREES
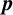 $\boldsymbol {p}$-GROUPS
$\boldsymbol {p}$-GROUPS
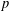 $p$-SUBGROUPS
$p$-SUBGROUPS
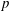 $p$-groups
$p$-groups