We are interested in dendrites for which all invariant measures of zero-entropy mappings have discrete spectrum, and we prove that this holds when the closure of the endpoint set of the dendrites is countable. This solves an open question which has been around for awhile, and almost completes the characterization of dendrites with this property.

In this paper we show that generic continuous Lebesgue measure-preserving circle maps have the s-limit shadowing property. In addition, we obtain that s-limit shadowing is a generic property also for continuous circle maps. In particular, this implies that classical shadowing, periodic shadowing and limit shadowing are generic in these two settings as well.

We prove that there exists a topologically mixing homeomorphism which is completely scrambled. We also prove that, for any integer $n\geq 1$, there is a continuum of topological dimension $n$ supporting a transitive completely scrambled homeomorphism and an $n$-dimensional compactum supporting a weakly mixing completely scrambled homeomorphism. This solves a 15-year-old open problem.

For dynamical systems with the shadowing property, we provide a method of approximation of invariant measures by ergodic measures supported on odometers and their almost one-to-one extensions. For a topologically transitive system with the shadowing property, we show that ergodic measures supported on odometers are dense in the space of invariant measures, and then ergodic measures are generic in the space of invariant measures. We also show that for every $c\geq 0$ and $\unicode[STIX]{x1D700}>0$ the collection of ergodic measures (supported on almost one-to-one extensions of odometers) with entropy between $c$ and $c+\unicode[STIX]{x1D700}$ is dense in the space of invariant measures with entropy at least $c$. Moreover, if in addition the entropy function is upper semi-continuous, then, for every $c\geq 0$, ergodic measures with entropy $c$ are generic in the space of invariant measures with entropy at least $c$.

We prove that when $f$ is a continuous self-map acting on a compact metric space $(X,d)$ that satisfies the shadowing property, then the set of irregular points (i.e., points with divergent Birkhoff averages) has full entropy. Using this fact, we prove that, in the class of $C^{0}$-generic maps on manifolds, we can only observe (in the sense of Lebesgue measure) points with convergent Birkhoff averages. In particular, the time average of atomic measures along orbits of such points converges to some Sinai–Ruelle–Bowen-like measure in the weak$^{\ast }$ topology. Moreover, such points carry zero entropy. In contrast, irregular points are non-observable but carry infinite entropy.

In the paper we study relations of rigidity, equicontinuity and pointwise recurrence between an invertible topological dynamical system (t.d.s.) 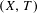$(X,T)$ and the t.d.s.  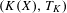$(K(X),T_{K})$ induced on the hyperspace 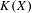$K(X)$ of all compact subsets of 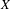$X$ , and provide some characterizations. Among other examples, we construct a minimal, non-equicontinuous, distal and uniformly rigid t.d.s. and a weakly mixing t.d.s. which induces dense periodic points on the hyperspace 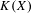$K(X)$ but itself does not have dense distal points, solving in that way a few open questions from earlier articles by Dong, and Li, Yan and Ye.

We study relations between transitivity, mixing and periodic points on dendrites. We prove that, when there is a point with dense orbit which is a cutpoint, periodic points are dense and there is a terminal periodic decomposition. We also show that it is possible that all periodic points except one (and points with dense orbit) are contained in the (dense) set of endpoints. It is also possible that a dynamical system is transitive but there is a unique periodic point which, in fact, is the unique fixed point. We also prove that on almost meshed continua (a class of continua containing topological graphs and dendrites with closed or countable set of endpoints), periodic points are dense if and only if they are dense for the map induced on the hyperspace of all non-empty compact subsets.

We provide a full characterization of relations between the shadowing property and the thick shadowing property. We prove that they are equivalent properties for non-wandering systems, the thick shadowing property is always a consequence of the shadowing property, and the thick shadowing property on the chain-recurrent set and the thick shadowing property are the same properties. We also provide a full characterization of the cases when for any family ${\mathcal{F}}$ with the Ramsey property an arbitrary sequence of points can be ${\it\varepsilon}$ -traced over a set from ${\mathcal{F}}$ .

Let ${ \mathcal{P} }_{G} $ be the family of all topologically mixing, but not exact self-maps of a topological graph $G$. It is proved that the infimum of topological entropies of maps from ${ \mathcal{P} }_{G} $ is bounded from below by $\log 3/ \Lambda (G)$, where $\Lambda (G)$ is a constant depending on the combinatorial structure of $G$. The exact value of the infimum on ${ \mathcal{P} }_{G} $ is calculated for some families of graphs. The main tool is a refined version of the structure theorem for mixing graph maps. It also yields new proofs of some known results, including Blokh’s theorem (topological mixing implies the specification property for maps on graphs).

In this paper we show that for every $n\geq 2$ there are minimal systems with perfect weakly mixing sets of order $n$ and all weakly mixing sets of order $n+ 1$ trivial. We present some relations between weakly mixing sets and topological sequence entropy; in particular, we prove that invertible minimal systems with non-trivial weakly mixing sets of order three always have positive topological sequence entropy. We also study relations between weak mixing of sets and other well-established notions from qualitative theory of dynamical systems like (regional) proximality, chaos and equicontinuity in a broad sense.

This article addresses some open questions about the relations between the topological weak mixing property and the transitivity of the map f×f2×⋯×fm, where f:X→X is a topological dynamical system on a compact metric space. The theorem stating that a weakly mixing and strongly transitive system is Δ-transitive is extended to a non-invertible case with a simple proof. Two examples are constructed, answering the questions posed by Moothathu [Diagonal points having dense orbit. Colloq. Math. 120(1) (2010), 127–138]. The first one is a multi-transitive non-weakly mixing system, and the second one is a weakly mixing non-multi-transitive system. The examples are special spacing shifts. The latter shows that the assumption of minimality in the multiple recurrence theorem cannot be replaced by weak mixing.