Inequalities on partial traces of positive semidefinite matrices are studied. Extensions of several existing inequalities on the determinant of partial traces are then obtained. Particularly, we improve a determinantal inequality given by Lin [Canad. Math. Bull. 59(2016)].

Given a complex semisimple Lie algebra $\mathfrak{g}=\mathfrak{k}+i\mathfrak{k}$ ( $\mathfrak{t}$ is a compact real form of $\mathfrak{g}$ ), let $\text{ }\pi \text{ }\text{:}\mathfrak{g}\to \mathfrak{h}$ be the orthogonal projection (with respect to the Killing form) onto the Cartan subalgebra $\mathfrak{h}:=\mathfrak{t}\text{+}i\mathfrak{t}$ , where $\mathfrak{t}$ is a maximal abelian subalgebra of $\mathfrak{k}$ . Given $x\,\in \,\mathfrak{g}$ , we consider $\text{ }\!\!\pi\!\!\text{ (Ad(}K\text{)}x)$ , where $K$ is the analytic subgroup $G$ corresponding to $\mathfrak{k}$ , and show that it is star-shaped. The result extends a result of Tsing. We also consider the generalized numerical range $f(\text{Ad(}K\text{)}x)$ , where $f$ is a linear functional on $\mathfrak{g}$ . We establish the star-shapedness of $f(\text{Ad(}K\text{)}x)$ for simple Lie algebras of type $B$ .

Let V be an n–dimensional inner product space over , let H be a subgroup of the symmetric group on {l,…, m}, and let x: H → be an irreducible character. Denote by (H) the symmetry class of tensors over V associated with H and x. Let K (T) ∈ End((H)) be the operator induced by T ∈ End(V), and let DK(T) be the derivation operator of T. The decomposable numerical range W*(DK(T)) of DK(T) is a subset of the classical numerical range W(DK(T)) of DK(T). It is shown that there is a closed star-shaped subset of complex numbers such that

⊆ W*(DK(T)) ⊆ W(DK(T)) = con

where conv denotes the convex hull of . In many cases, the set is convex, and thus the set inclusions are actually equalities. Some consequences of the results and related topics are discussed.

We generalize the well-known result that a square traceless complex matrix is unitarily similar to a matrix with zero diagonal to arbitrary connected semisimple complex Lie groups 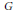$G$ and their Lie algebras 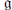$\mathfrak{g}$ under the action of a maximal compact subgroup $K$ of 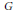$G$ . We also introduce a natural partial order on 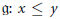$\mathfrak{g}:\,x\,\le y$ if 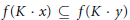$f(K\,\cdot \,x)\,\subseteq \,f(K\,\cdot \,y)$ for all 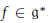$f\,\in \,{{\mathfrak{g}}^{*}}$ , the complex dual of 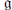$\mathfrak{g}$ . This partial order is $K$ -invariant and induces a partial order on the orbit space 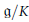$\mathfrak{g}/K$ . We prove that, under some restrictions on 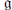$\mathfrak{g}$ , the set 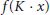$f(K\,\cdot \,x)$ is star-shaped with respect to the origin.

Westwick's convexity theorem on the numerical range is generalized in the context of compact connected Lie groups.

A unified formulation is given to various generalizations of the classical numerical range including the $c$ -numerical range, congruence numerical range, $q$ -numerical range and von Neumann range. Attention is given to those cases having connections with classical simple real Lie algebras. Convexity and inclusion relation involving those generalized numerical ranges are investigated. The underlying geometry is emphasized.

Thompson's famous theorems on singular values–diagonal elements of the orbit of an n×n matrix A under the action (1) U(n) [otimes] U(n) where A is complex, (2) SO(n) [otimes] SO(n), where A is real, (3) O(n) [otimes] O(n) where A is real are fully examined. Coupled with Kostant's result, the real semi-simple Lie algebra [sfr ][ofr ]n, n yields (2) and hence (3) and the sufficient part (the hard part) of (1). In other words, the curious subtracted term(s) are well explained. Although the diagonal elements corresponding to (1) do not form a convex set in [Copf]n, the projection of the diagonal elements into ℝn (or iℝn) is convex and the characterization of the projection is related to weak majorization. An elementary proof is given for this hidden convexity result. Equivalent statements in terms of the Hadamard product are also given. The real simple Lie algebra [sfr ][ufr ]n, n shows that such a convexity result fits into the framework of Kostant's result. Convexity properties and torus relations are studied. Thompson's results on the convex hull of matrices (complex or real) with prescribed singular values, as well as Hermitian matrices (real symmetric matrices) with prescribed eigenvalues, are generalized in the context of Lie theory. Also considered are the real simple Lie algebras [sfr ][ofr ]p, q and [sfr ][ofr ]p, q, p < q, which yield the rectangular cases. It is proved that the real part and the imaginary part of the diagonal elements of complex symmetric matrices with prescribed singular values are identical to a convex set in ℝn and the characterization is related to weak majorization. The convex hull of complex symmetric matrices and the convex hull of complex skew symmetric matrices with prescribed singular values are given. Some questions are asked.

For a real vector space V acted on by a group K and fixed x and y in V, we consider the problem of finding the minimum (respectively, maximum) distance, relative to a K-invariant convex function on V, between x and elements of the convex hull of the K-orbit of y. We solve this problem in the case where V is a Euclidean space and K is a finite reflection group acting on V. Then we use this result to obtain an analogous result in the case where K is a maximal compact subgroup of a reductive group G with adjoint action on the vector component ρ of a Cartan decomposition of Lie G. Our results generalize results of Li and Tsing and of Cheng concerning distances to the convex hulls of matrix orbits.