We study optimal dimensionless inequalities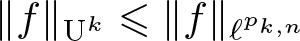

\begin{equation*} \|f\|_{\textrm{U}^k} \leqslant \|f\|_{\ell^{p_{k,n}}} \end{equation*}

that hold for all functions 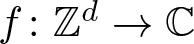$f\colon\mathbb{Z}^d\to\mathbb{C}$ supported in 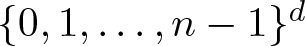$\{0,1,\ldots,n-1\}^d$ and estimates

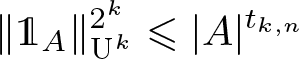\begin{equation*} \|\mathbb{1}_A\|_{\textrm{U}^k}^{2^k}\leqslant |A|^{t_{k,n}} \end{equation*}

that hold for all subsets A of the same discrete cubes. A general theory, analogous to the work of de Dios Pont, Greenfeld, Ivanisvili, and Madrid, is developed to show that the critical exponents are related by 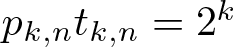$p_{k,n} t_{k,n} = 2^k$. This is used to prove the three main results of the article:

• • an explicit formula for $t_{k,2}$, which generalizes a theorem by Kane and Tao,

• • two-sided asymptotic estimates for $t_{k,n}$ as $n\to\infty$ for a fixed $k\geqslant2$, which generalize a theorem by Shao, and

• • a precise asymptotic formula for $t_{k,n}$ as $k\to\infty$ for a fixed $n\geqslant2$.

We prove almost everywhere convergence of continuous-time quadratic averages with respect to two commuting $\mathbb {R}$-actions, coming from a single jointly measurable measure-preserving $\mathbb {R}^2$-action on a probability space. The key ingredient of the proof comes from recent work on multilinear singular integrals; more specifically, from the study of a curved model for the triangular Hilbert transform.

Several results in the existing literature establish Euclidean density theorems of the following strong type. These results claim that every set of positive upper Banach density in the Euclidean space of an appropriate dimension contains isometric copies of all sufficiently large elements of a prescribed family of finite point configurations. So far, all results of this type discussed linear isotropic dilates of a fixed point configuration. In this paper, we initiate the study of analogous density theorems for families of point configurations generated by anisotropic dilations, i.e., families with power-type dependence on a single parameter interpreted as their size. More specifically, we prove nonisotropic power-type generalizations of a result by Bourgain on vertices of a simplex, a result by Lyall and Magyar on vertices of a rectangular box, and a result on distance trees, which is a particular case of the treatise of distance graphs by Lyall and Magyar. Another source of motivation for this paper is providing additional evidence for the versatility of the approach stemming from the work of Cook, Magyar, and Pramanik and its modification used recently by Durcik and the present author. Finally, yet another purpose of this paper is to single out anisotropic multilinear singular integral operators associated with the above combinatorial problems, as they are interesting on their own.

We prove that sets with positive upper Banach density in sufficiently large dimensions contain congruent copies of all sufficiently large dilates of three specific higher-dimensional patterns. These patterns are: 2n vertices of a fixed n-dimensional rectangular box, the same vertices extended with n points completing three-term arithmetic progressions, and the same vertices extended with n points completing three-point corners. Our results provide common generalizations of several Euclidean density theorems from the literature.

We study double ergodic averages with respect to two general commuting transformations and establish a sharp quantitative result on their convergence in the norm. We approach the problem via real harmonic analysis, using recently developed methods for bounding multilinear singular integrals with certain entangled structure. A byproduct of our proof is a bound for a two-dimensional bilinear square function related to the so-called triangular Hilbert transform.

The so-called triangular Hilbert transform is an elegant trilinear singular integral form which specializes to many well-studied objects of harmonic analysis. We investigate $L^{p}$ bounds for a dyadic model of this form in the particular case when one of the functions on which it acts is essentially one dimensional. This special case still implies dyadic analogues of boundedness of the Carleson maximal operator and of the uniform estimates for the one-dimensional bilinear Hilbert transform.

We study double averages along orbits for measure-preserving actions of $\mathbb{A}^{{\it\omega}}$, the direct sum of countably many copies of a finite abelian group $\mathbb{A}$. We show an $\text{L}^{p}$ norm-variation estimate for these averages, which in particular re-proves their convergence in $\text{L}^{p}$ for any finite $p$ and for any choice of two $\text{L}^{\infty }$ functions. The result is motivated by recent questions on quantifying convergence of multiple ergodic averages.