Universal masking for healthcare workers and patients in hospitals was adopted to combat coronavirus disease 2019 (COVID-19), with compliance rates of 100% and 75.9%, respectively. Zero rates of nosocomial influenza A, influenza B, and respiratory syncytial virus infection were achieved from February to April 2020, which was significantly lower than the corresponding months in 2017–2019.

The purpose of the study was to determine the incidence of cardiovascular disease (CVD) among people living with human immunodeficiency virus (HIV)/acquired immunodeficiency syndrome (PLWHA) in Taiwan. PLWHA were identified from the Taiwan Centers for Disease Control HIV Surveillance System between 2000 and 2014. To examine the effect of active antiretroviral therapy (HAART) on CVD incidence, incidence densities and standardised incidence rates (SIRs) of CVD were calculated after stratifying PLWHA by HAART. Of 26 272 PLWHA (mean age, 32.3 years) identified, 73.4% received HAART. Compared with general population, SIRs (95% confidence interval) were higher for incident coronary artery disease (1.11 (1.04–1.19)), percutaneous coronary intervention (1.32 (1.18–1.47)), coronary artery bypass surgery (1.47 (1.29–1.66)), sudden cardiac death (3.01 (2.39–3.73)), heart failure (1.50 (1.31–1.70)) and chronic kidney disease (1.95 (1.81–2.10)), but was lower for incident atrial fibrillation (0.53 (0.37–0.73)). Considering the effect of HAART on incident CVD, the SIRs for all-cause, ischaemic and haemorrhagic stroke were higher in PLWHA who did not receive HAART, but were lower in PLWHA who received HAART. PLWHA had higher risks of incident coronary artery disease, percutaneous coronary intervention, coronary artery bypass surgery, sudden cardiac death, heart failure and chronic kidney disease. HAART reduces risks of incident CVD in PLWHA.

Forty-eight different Ag–Al–Zr ternary alloys were prepared in various compositions to determine the metallic glass region in the Ag–Al–Zr ternary system. Experimental results indicated that the metallic glass region in the Ag–Al–Zr ternary system is Ag20–30Al10–30Zr50–60. The Ag20Al30Zr50 and Ag30Al20Zr50 alloys are supposed to have the best glass-forming ability in the Ag–Al–Zr ternary system. The phase equilibria of the Ag–Al–Zr ternary system at 773 K (500 °C) were investigated and compared with the metallic glass region results in the Ag–Al–Zr ternary system. Ternary isothermal sections of the Ag–Al–Zr system at 773 K (500 °C) were established and two ternary intermetallic phases were observed in this isothermal section.

Modulation of the cellular response by the administration of probiotic bacteria may be an effective strategy for preventing or inhibiting tumour growth. We orally pre-inoculated mice with probiotics Lactobacillus acidophilus NCFM (La) for 14 d. Subcutaneous dorsal-flank tumours and segmental orthotopic colon cancers were implanted into mice using CT-26 murine colon adenocarcinoma cells. On day 28 after tumour initiation, the lamina propria of the colon, mesenteric lymph nodes (MLN) and spleen were harvested and purified for flow cytometry and mRNA analyses. We demonstrated that La pre-inoculation reduced tumour volume growth by 50·3 %, compared with untreated mice at 28 d after tumour implants (2465·5 (sem 1290·4) v. 4950·9 (sem 1689·3) mm3, P < 0·001). Inoculation with La reduced the severity of colonic carcinogenesis caused by CT-26 cells, such as level of colonic involvement and structural abnormality of epithelial/crypt damage. Moreover, La enhanced apoptosis of CT-26 cells both in dorsal-flank tumour and segmental orthotopic colon cancer, and the mean counts of apoptotic body were higher in mice pre-inoculated with La (P < 0·05) compared with untreated mice. La pre-inoculation down-regulated the CXCR4 mRNA expressions in the colon, MLN and extra-intestinal tissue, compared with untreated mice (P < 0·05). In addition, La pre-inoculation reduced the mean fluorescence index of MHC class I (H-2Dd, -Kd and -Ld) in flow cytometry analysis. Taken together, these findings suggest that probiotics La may play a role in attenuating tumour growth during CT-26 cell carcinogenesis. The down-regulated expression of CXCR4 mRNA and MHC class I, as well as increasing apoptosis in tumour tissue, indicated that La may be associated with modulating the cellular response triggered by colon carcinogenesis.

The objective of this research is to obtain uniform vacuum-deposition triclinic phase II crystal of titanyl phthalocyanine (α-TiOPc) films from various TiOPc crystal forms. The crystal structure and morphology of vacuum-deposited TiOPc films can be manipulated by deposition rate and substrate temperature. Crystal structure was determined by X-ray diffraction (XRD). Thin film morphology was analyzed by scanning electron microscope (SEM). Highly ordered α-TiOPc film with an edge-on molecular orientation was deposited on octadecyltrichlorosilane (OTS) treated Si/SiO2 surface. All TiOPc crystal forms, such as amorphous, α and γ phases, provided the triclinic phase II crystal of TiOPc. The full width at half maximum (FWHM) of the peak at 7.5 degree in XRD spectra was 0.23, 0.27 and 0.29 for γ, α and amorphous powder when substrate temperature maintained at 180°C, respectively. The FWHM of the 7.5 degree peak can be achieved 0.22 deposited from all crystal forms at elevated temperature higher than 220°C. The α-TiOPc deposition film exhibited an excellent p-type semiconducting behavior in air with dense packing structure due to the close π–π molecular packing. The devices, field-effect mobility range from 0.02 to 0.26 cm2/V s depending on various process parameters. The on/off current ratio (Ion/Ioff) is over 105. The TiOPc OTFTs will be applied as multi-parameter gas sensor in the near future.

Let f(x) be integrable L(0, 2π) and periodic with period 2π, and let ψ(t) be the conjugate function of with respect to the variable t, where x is onsidered as an arbitrary constant. The following theorems are due to K. K. Chen (1), (2), pp. 111–124.

This study examined NADPH-d and nNOS expression in the SCG of hamsters. By light microscopy, numerous NADPH-d/NOS positive processes were widely distributed in the ganglion. Ultrastructurally, the NADPH-d reaction product was associated with the membranous organelles of neuronal soma, dendrites, myelinated fibres, small granular cells, and axon profiles bearing agranular vesicles. The NOS immunoreaction product, on the other hand, was localised in the cytoplasm of principal neurons and dendrites. Some of the NADPH-d/NOS labelled processes formed junctional contacts including synapses or zonulae adherentia. Compared with the neurons, the nonneuronal cells in the ganglion, namely, macrophages, satellite cells and endothelial cells were labelled by NADPH-d but devoid of nNOS immunoreaction product. The results suggest that the NADPH-d/NOS positive fibres in the SCG originate not only from the projecting fibres of the lateral horns of thoracic spinal cord, but also from the principal neurons and small granular cells; some may represent visceral afferent fibres. Electron microscopic morphometry has shown that about 67% of the principal neurons contain NADPH-d reaction product, and that the majority were small to medium sized neurons based on cross-sectional areas in image analysis. On the basis of the present morphological study, it is concluded NO is produced by some local neurons and possibly some nonneuronal cells in the SCG as well as some fibres of extrinsic origin. In this connection, NO may serve either as a neurotransmitter or neuromodulator.

1. P. Heywood [3] proved the following theorems:

Theorem A. If 0 ≦ λ < 2, if xy−1g(x) ε L(0, π), and if

for n = 1, 2, 3,…, then the series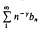is convergent.

Theorem B. If 0 ≦ λ < 1, if xy−1f(x)ε L(0, π), and if

for n = 1, 2, 3,…, then the series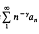n−yanis convergent.

In a previous paper (3) generalizations of M. Riesz's theorem by the method of asymptotic approximation have been given. The present paper is concerned with further generalizations for even and odd functions. In Section 3, we consider a generalization of a theorem due to Zygmund: If (10, p. 254). The results in this paper include generalizations of results by K. K. Chen (2) and T. M. Flett (4, Theorems 1, 2) as important special cases.