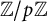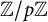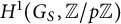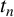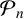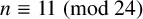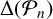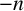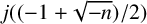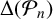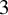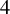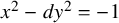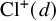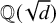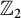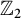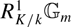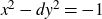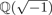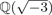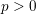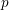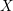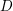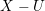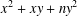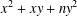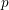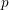Refine search
Actions for selected content:
22 results
Rigid meromorphic cocycles for orthogonal groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 30 September 2025, e160
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Elliptic curves and spin
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 3 / November 2025
- Published online by Cambridge University Press:
- 11 July 2025, pp. 519-539
- Print publication:
- November 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On tame
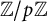 ${\mathbb {Z}}/p{\mathbb {Z}}$-extensions with prescribed ramification
${\mathbb {Z}}/p{\mathbb {Z}}$-extensions with prescribed ramification
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 13 June 2023, pp. 40-48
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON DISCRIMINANTS OF MINIMAL POLYNOMIALS OF THE RAMANUJAN
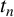 $t_n$ CLASS INVARIANTS
$t_n$ CLASS INVARIANTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 11 April 2023, pp. 264-275
- Print publication:
- October 2023
-
- Article
- Export citation
The 8-rank of the narrow class group and the negative Pell equation
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 21 June 2022, e46
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On metabelian 2-class field towers over
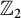 $\mathbb Z_2$-extensions of real quadratic fields
$\mathbb Z_2$-extensions of real quadratic fields
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 06 October 2021, pp. 795-805
- Print publication:
- September 2022
-
- Article
- Export citation
Explicit methods for the Hasse norm principle and applications to An and Sn extensions
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 22 April 2021, pp. 489-529
- Print publication:
- May 2022
-
- Article
-
- You have access
- Open access
- Export citation
Redei reciprocity, governing fields and negative Pell
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 19 April 2021, pp. 627-654
- Print publication:
- May 2022
-
- Article
-
- You have access
- Open access
- Export citation
CLASS NUMBER FORMULA FOR DIHEDRAL EXTENSIONS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 2 / May 2020
- Published online by Cambridge University Press:
- 21 May 2019, pp. 323-353
- Print publication:
- May 2020
-
- Article
-
- You have access
- Export citation
On the Schertz Conjecture
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 3 / August 2019
- Published online by Cambridge University Press:
- 08 February 2019, pp. 837-845
-
- Article
- Export citation
Binary quadratic forms and ray class groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 23 January 2019, pp. 695-720
- Print publication:
- April 2020
-
- Article
- Export citation
Pólya S3-extensions of ℚ
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 1421-1433
- Print publication:
- December 2019
-
- Article
- Export citation
HIGHER IDELES AND CLASS FIELD THEORY
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 236 / December 2019
- Published online by Cambridge University Press:
- 02 October 2018, pp. 214-250
- Print publication:
- December 2019
-
- Article
-
- You have access
- HTML
- Export citation
Duality for relative logarithmic de Rham–Witt sheaves and wildly ramified class field theory over finite fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 6 / June 2018
- Published online by Cambridge University Press:
- 07 May 2018, pp. 1306-1331
- Print publication:
- June 2018
-
- Article
- Export citation
Construction of ray-class fields by smaller generators and their applications
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 4 / August 2017
- Published online by Cambridge University Press:
- 20 March 2017, pp. 781-812
- Print publication:
- August 2017
-
- Article
- Export citation
Some applications of eta-quotients
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 22 March 2016, pp. 565-578
- Print publication:
- June 2016
-
- Article
- Export citation
ALGORITHMS FOR GALOIS EXTENSIONS OF GLOBAL FUNCTION FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 17 February 2016, pp. 513-515
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
THE PROPORTION OF FAILURES OF THE HASSE NORM PRINCIPLE
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 22 January 2016, pp. 337-347
- Print publication:
- 2016
-
- Article
- Export citation
REPRESENTATIONS OF INTEGERS BY THE BINARY QUADRATIC FORM
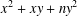 $x^{2}+xy+ny^{2}$
$x^{2}+xy+ny^{2}$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 17 November 2015, pp. 182-191
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
Hecke characters associated to Drinfeld modular forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 11 / November 2015
- Published online by Cambridge University Press:
- 01 June 2015, pp. 2006-2058
- Print publication:
- November 2015
-
- Article
- Export citation