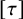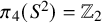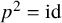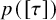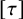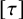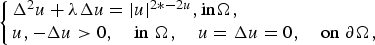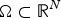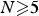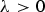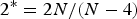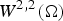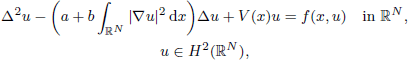Refine search
Actions for selected content:
9 results
Normalized ground states for a biharmonic Choquard equation with exponential critical growth
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 03 September 2025, pp. 1-35
-
- Article
- Export citation
Biharmonic almost complex structures
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 31 March 2023, e25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Existence, non-existence and blow-up behaviour of minimizers for the mass-critical fractional non-linear Schrödinger equations with periodic potentials
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 13 January 2020, pp. 3252-3292
- Print publication:
- December 2020
-
- Article
- Export citation
EXISTENCE AND UNIQUENESS OF WEAK AND CLASSICAL SOLUTIONS FOR A FOURTH-ORDER SEMILINEAR BOUNDARY VALUE PROBLEM
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 61 / Issue 3 / July 2019
- Published online by Cambridge University Press:
- 19 August 2019, pp. 305-319
-
- Article
-
- You have access
- Export citation
Existence and multiplicity of positive solutions for a fourth-order elliptic equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 28 January 2019, pp. 1053-1069
- Print publication:
- April 2020
-
- Article
- Export citation
Infinitely Many Solutions for Schrödinger–Kirchhoff-Type Fourth-Order Elliptic Equations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 30 January 2017, pp. 1003-1020
-
- Article
- Export citation
SOME REMARKS ON THE
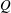 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}Q$ CURVATURE TYPE PROBLEM ON
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}Q$ CURVATURE TYPE PROBLEM ON 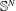 $\mathbb{S}^N$
$\mathbb{S}^N$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 16 June 2014, pp. 127-143
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
ON A CLASS OF SOBOLEV FUNCTIONS AND ITS APPLICATIONS TO HIGHER-ORDER ELLIPTIC EQUATIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 3 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 405-417
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
A posteriori error estimates for elliptic boundary-value problems
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 39 / Issue 2 / October 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 159-168
- Print publication:
- October 1985
-
- Article
-
- You have access
- Export citation