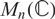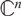Refine search
Actions for selected content:
14 results
The algebraic numerical range as a spectral set in Banach algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 17 February 2025, pp. 1-25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the convexity of the quaternionic essential numerical range
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 15 May 2024, pp. 838-851
-
- Article
- Export citation
HERMITIANS IN MATRIX ALGEBRAS WITH OPERATOR NORM – II
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 10 June 2021, pp. 376-396
- Print publication:
- May 2022
-
- Article
- Export citation
NUMERICAL RANGE AND POSITIVE BLOCK MATRICES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 11 June 2020, pp. 69-77
- Print publication:
- February 2021
-
- Article
- Export citation
HERMITIANS IN MATRIX ALGEBRAS WITH OPERATOR NORM
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 27 April 2020, pp. 280-290
- Print publication:
- May 2021
-
- Article
- Export citation
Escaping a Neighborhood Along a Prescribed Sequence in Lie Groups and Banach Algebras
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 02 October 2019, pp. 484-505
- Print publication:
- September 2020
-
- Article
-
- You have access
- Export citation
On a second numerical index for Banach spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 28 January 2019, pp. 1003-1051
- Print publication:
- April 2020
-
- Article
- Export citation
Numerical Ranges in II1 Factors
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 16 March 2017, pp. 31-55
-
- Article
- Export citation
Hyponormal operators on uniformly smooth spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 50 / Issue 1 / February 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 150-159
- Print publication:
- February 1991
-
- Article
-
- You have access
- Export citation
Subsets characterizing the closure of the numerical range
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 40 / Issue 1 / February 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-4
- Print publication:
- February 1986
-
- Article
-
- You have access
- Export citation
Subspaces associated with boundary points of the numerical range
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 39 / Issue 1 / August 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 21-27
- Print publication:
- August 1985
-
- Article
-
- You have access
- Export citation
On numerical ranges of generalized derivations and related properties
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 36 / Issue 1 / February 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 134-142
- Print publication:
- February 1984
-
- Article
-
- You have access
- Export citation
Denseness of operators which attain their numerical radius
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 36 / Issue 1 / February 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 130-133
- Print publication:
- February 1984
-
- Article
-
- You have access
- Export citation
Linearity and weak convergence on the boundary of numerical range
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 35 / Issue 2 / October 1983
- Published online by Cambridge University Press:
- 09 April 2009, pp. 221-226
- Print publication:
- October 1983
-
- Article
-
- You have access
- Export citation