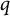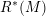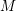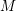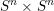Refine search
Actions for selected content:
9 results
Characteristic numbers of manifold bundles over spheres and positive curvature via block bundles
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 26 August 2025, e138
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Kudla–Millson form via the Mathai–Quillen formalism
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 05 October 2023, pp. 1638-1663
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Holomorphic one-forms, fibrations over the circle, and characteristic numbers of Kähler manifolds
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 26 February 2021, pp. 95-103
- Print publication:
- January 2022
-
- Article
-
- You have access
- Open access
- Export citation
Tautological rings for high-dimensional manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 4 / April 2017
- Published online by Cambridge University Press:
- 13 March 2017, pp. 851-866
- Print publication:
- April 2017
-
- Article
- Export citation
ON DIFFERENTIAL CHARACTERISTIC CLASSES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 04 December 2014, pp. 30-47
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
LOOP GROUPS, STRING CLASSES AND EQUIVARIANT COHOMOLOGY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 90 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 22 March 2011, pp. 109-127
- Print publication:
- February 2011
-
- Article
-
- You have access
- Export citation
Non-embeddings of the real flag manifolds RF (1, 1, n – 2)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 66 / Issue 1 / February 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 51-55
- Print publication:
- February 1999
-
- Article
-
- You have access
- Export citation
The Vanishing problem of the string class with degree 3
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 65 / Issue 1 / August 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 129-142
- Print publication:
- August 1998
-
- Article
-
- You have access
- Export citation
On the vanishing problem of string classes
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 61 / Issue 2 / October 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 258-266
- Print publication:
- October 1996
-
- Article
-
- You have access
- Export citation