An element of a group is called strongly reversible or strongly real if it can be expressed as a product of two involutions. We provide necessary and sufficient conditions for an element of $\mathrm{SL}(n,\mathbb{C})$ to be a product of two involutions. In particular, we classify the strongly reversible conjugacy classes in $\mathrm{SL}(n,\mathbb{C})$.

An element of a group is called reversible if it is conjugate to its own inverse. Reversible elements are closely related to strongly reversible elements, which can be expressed as a product of two involutions. In this paper, we classify the reversible and strongly reversible elements in the quaternionic special linear group $ \mathrm {SL}(n,\mathbb {H})$ and quaternionic projective linear group $ \mathrm {PSL}(n,\mathbb {H})$. We prove that an element of $ \mathrm {SL}(n,\mathbb {H})$ (resp. $ \mathrm {PSL}(n,\mathbb {H})$) is reversible if and only if it is a product of two skew-involutions (resp. involutions).

Let p be a prime and let 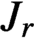$J_r$ denote a full $r \times r$ Jordan block matrix with eigenvalue 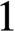$1$ over a field F of characteristic p. For positive integers r and s with 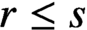$r \leq s$, the Jordan canonical form of the $r s \times r s$ matrix $J_{r} \otimes J_{s}$ has the form $J_{\lambda _1} \oplus J_{\lambda _2} \oplus \cdots \oplus J_{\lambda _{r}}$. This decomposition determines a partition 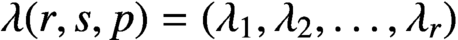$\lambda (r,s,p)=(\lambda _1,\lambda _2,\ldots , \lambda _{r})$ of 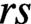$r s$. Let $n_1, \ldots , n_k$ be the multiplicities of the distinct parts of the partition and set 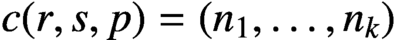$c(r,s,p)=(n_1,\ldots ,n_k)$. Then 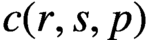$c(r,s,p)$ is a composition of r. We present a new bottom-up algorithm for computing 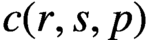$c(r,s,p)$ and 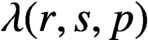$\lambda (r,s,p)$ directly from the base-p expansions for r and s.

We present conditions for a set of matrices satisfying a permutation identity to be simultaneously triangularizable. As applications of our results, we generalize Radjavi’s result on triangularization of matrices with permutable trace and results by Yan and Tang on linear triangularization of polynomial maps.

We prove that if $\mathfrak{s}$ is a solvable Lie algebra of matrices over a field of characteristic 0 and $A\in \mathfrak{s}$, then the semisimple and nilpotent summands of the Jordan–Chevalley decomposition of $A$ belong to $\mathfrak{s}$ if and only if there exist $S,N\in \mathfrak{s}$, $S$ is semisimple, $N$ is nilpotent (not necessarily $[S,N]=0$) such that $A=S+N$.

We show that the product rank of the $3\,\times \,3$ determinant ${{\det }_{3}}$ is $5$ , and the product rank of the $3\,\times \,3$ permanent $\text{per}{{\text{m}}_{3}}$ is $4$ . As a corollary, we obtain that the tensor rank of ${{\det }_{3}}$ is $5$ and the tensor rank of $\text{per}{{\text{m}}_{3}}$ is $4$ . We show moreover that the border product rank of $\text{per}{{\text{m}}_{3}}$ is larger than $n$ for any $n\,\ge \,3$ .

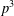The class of almost completely decomposable groups with a critical typeset of type $(2,2)$ and a homocyclic regulator quotient of exponent $p^{3}$ is shown to be of bounded representation type. There are only $16$ isomorphism at $p$ types of indecomposables, all of rank $8$ or lower.

Let $G$ be a finite group. We classify $G$-equivariant flow equivalence of non-trivial irreducible shifts of finite type in terms of

(i) elementary equivalence of matrices over $ZG$ and

(ii) the conjugacy class in $ZG$ of the group of G-weights of cycles based at a fixed vertex.

In the case $G = Z/2$, we have the classification for twistwise flow equivalence. We include some algebraic results and examples related to the determination of $E(ZG)$ equivalence, which involves $K_1(ZG)$.

An $n\times n$ matrix is said to be totally nonnegative if every minor of $A$ is nonnegative. In this paper we completely characterize all possible Jordan canonical forms of irreducible totally nonnegative matrices. Our approach is mostly combinatorial and is based on the study of weighted planar diagrams associated with totally nonnegative matrices.

Real matrix pairs (A,H) satisfying det H ≠ 0, HT = εH, and HA - ηATH, where ε, η take the values +1 or —1, are considered. It is shown that maximal A-invariant H-neutral subspaces have the same dimension (depending on ε and η), called the order of neutrality of the pair (A, H). The order of neutrality of definitizable pairs is investigated. In particular, this concept is used to obtain lower bounds for the number of pure imaginary eigenvalues of low rank perturbations of definitizable pairs when (ε,η) = (1, - 1 ) and when (ε,η) = (—1,—1).

Let T be a linear transformation acting on the space of n x n complex matrices. Let G(k) be the set of all hermitian matrices with k positive and n — k negative eigenvalues. Let T map some indefinite inertia class G(k) onto itself. We classify all such T. The possibilities are congruence, congruence followed by transposition, and, if n = 2k, it is possible that — T can be a congruence or a congruence followed by transposing. In other words, negation is an admissible transformation when n = 2k.

The relationship between properties of the generalized inverse of A, A†, and of the adjoint of A, A*, are studied. The property that A†A and AA† commute, called (E4), is investigated. (E4) generalizes the property of A being EPr. A canonical form and a formula for A† are given if a matrix A is (E4). Results are in a Hilbert space setting whenever possible. Examples are given.