Using a perturbation result established by Galatolo and Lucena [Spectral gap and quantitative statistical stability for systems with contracting fibers and Lorenz-like maps. Discrete Contin. Dyn. Syst. 40(3) (2020), 1309–1360], we obtain quantitative estimates on the continuity of the invariant densities and entropies of the physical measures for some families of piecewise expanding maps. We apply these results to a family of two-dimensional tent maps.

The exponential ordering is exploited in the context of nonautonomous delay systems, inducing monotone skew-product semiflows under less restrictive conditions than usual. Some dynamical concepts linked to the order, such as semiequilibria, are considered for the exponential ordering, with implications for the determination of the presence of uniform persistence or the existence of global attractors. Also, some important conclusions on the long-term dynamics and attraction are obtained for monotone and sublinear delay systems for this ordering. The results are then applied to almost periodic Nicholson systems and new conditions are given for the existence of a unique almost periodic positive solution which asymptotically attracts every other positive solution.

Let f be a smooth symplectic diffeomorphism of ${\mathbb R}^2$ admitting a (non-split) separatrix associated to a hyperbolic fixed point. We prove that if f is a perturbation of the time-1 map of a symplectic autonomous vector field, this separatrix is accumulated by a positive measure set of invariant circles. However, we provide examples of smooth symplectic diffeomorphisms with a Lyapunov unstable non-split separatrix that are not accumulated by invariant circles.

We construct two planar homoeomorphisms $f$ and $g$ for which the origin is a globally asymptotically stable fixed point whereas for $f \circ g$ and $g \circ f$ the origin is a global repeller. Furthermore, the origin remains a global repeller for the iterated function system generated by $f$ and $g$ where each of the maps appears with a certain probability. This planar construction is also extended to any dimension $>$2 and proves for first time the appearance of the dynamical Parrondo's paradox in odd dimensions.

We consider products of an independent and identically distributed sequence in a set $\{f_1,\ldots ,f_m\}$ of orientation-preserving diffeomorphisms of the circle. We can naturally associate a Lyapunov exponent 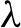$\lambda $. Under few assumptions, it is known that 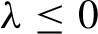$\lambda \leq 0$ and that the equality holds if and only if $f_1,\ldots ,f_m$ are simultaneously conjugated to rotations. In this paper, we state a quantitative version of this fact in the case where $f_1,\ldots ,f_m$ are 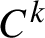$C^k$ perturbations of rotations with rotation numbers $\rho (f_1),\ldots ,\rho (f_m)$ satisfying a simultaneous diophantine condition in the sense of Moser [On commuting circle mappings and simultaneous diophantine approximations. Math. Z. 205(1) (1990), 105–121]: we give a precise estimate of 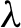$\lambda $ (Taylor expansion) and we prove that there exist a diffeomorphism g and rotations 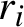$r_i$ such that 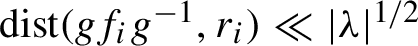$\mbox {dist}(gf_ig^{-1},r_i)\ll |\lambda |^{{1}/{2}}$ for 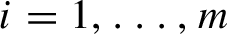$i=1,\ldots , m$. We also state analogous results for random products of $2\times 2$ matrices, without any diophantine condition.

We explore new connections between the dynamics of conservative partially hyperbolic systems and the geometric measure-theoretic properties of their invariant foliations. Our methods are applied to two main classes of volume-preserving diffeomorphisms: fibered partially hyperbolic diffeomorphisms and center-fixing partially hyperbolic systems. When the center is one-dimensional, assuming the diffeomorphism is accessible, we prove that the disintegration of the volume measure along the center foliation is either atomic or Lebesgue. Moreover, the latter case is rigid in dimension three (this does not require accessibility): the center foliation is actually smooth and the diffeomorphism is smoothly conjugate to an explicit rigid model. A partial extension to fibered partially hyperbolic systems with compact fibers of any dimension is also obtained. A common feature of these classes of diffeomorphisms is that the center leaves either are compact or can be made compact by taking an appropriate dynamically defined quotient. For volume-preserving partially hyperbolic diffeomorphisms whose center foliation is absolutely continuous, if the generic center leaf is a circle, then every center leaf is compact.

It is well known that along any stable manifold the dynamics travels with an exponential rate. Moreover, this rate is close to the slowest exponential rate along the stable direction of the linearization, provided that the nonlinear part is sufficiently small. In this note, we show that whenever there is also a fastest finite exponential rate along the stable direction of the linearization, similarly we can establish a lower bound for the speed of the nonlinear dynamics along the stable manifold. We consider both cases of discrete and continuous time, as well as a nonuniform exponential behaviour.

Let $M$ and $N$ be admissible Hausdorff topological spaces endowed with admissible families of open coverings. Assume that $\mathcal{S}$ is a semigroup acting on both $M$ and $N$ . In this paper we study the behavior of limit sets, prolongations, prolongational limit sets, attracting sets, attractors, and Lyapunov stable sets (all concepts defined for the action of the semigroup $\mathcal{S}$ ) under equivariant maps and semiconjugations from $M$ to $N$ .

We present a well-posed and discretely stable perfectly matched layer for the anisotropic (and isotropic) elastic wave equations without first re-writing the governing equations as a first order system. The new model is derived by the complex coordinate stretching technique. Using standard perturbation methods we show that complex frequency shift together with a chosen real scaling factor ensures the decay of eigen-modes for all relevant frequencies. To buttress the stability properties and the robustness of the proposed model, numerical experiments are presented for anisotropic elastic wave equations. The model is approximated with a stable node-centered finite difference scheme that is second order accurate both in time and space.