We improve a previous result about the local energy decay for the damped wave equation on $\mathbb{R}^{d}$ . The problem is governed by a Laplacian associated with a long-range perturbation of the flat metric and a short-range absorption index. Our purpose is to recover the decay ${\mathcal{O}}(t^{-d+\unicode[STIX]{x1D700}})$ in the weighted energy spaces. The proof is based on uniform resolvent estimates, given by an improved version of the dissipative Mourre theory. In particular, we have to prove the limiting absorption principle for the powers of the resolvent with inserted weights.

The theory of the spectral shift function is extended to the case where only the difference of some powers of the resolvents of self-adjoint operators belongs to the trace class. As an example, a pair of Dirac operators is considered.

Voiculescu has previously established the uniqueness of the wave operator for the problem of ${{\mathcal{C}}^{(0)}}$ -perturbation of commuting tuples of self-adjoint operators in the case where the norm ideal $\mathcal{C}$ has the property ${{\lim }_{n\,\to \,\infty }}\,{{n}^{-1/2}}\,\left\| {{P}_{n}} \right\|\mathcal{C}\,=\,0$ , where $\{{{P}_{n}}\}$ is any sequence of orthogonal projections with rank $({{P}_{n}})\,=\,n$ . We prove that the same uniqueness result holds true so long as $\mathcal{C}$ is not the trace class. (It is well known that there is no such uniqueness in the case of trace-class perturbation.)

We obtain a new representation for the solution to the operator Sylvester equation in the form of a Stieltjes operator integral. We also formulate new sufficient conditions for the strong solvability of the operator Riccati equation that ensures the existence of reducing graph subspaces for block operator matrices. Next, we extend the concept of the Lifshits-Krein spectral shift function associated with a pair of self-adjoint operators to the case of pairs of admissible operators that are similar to self-adjoint operators. Based on this new concept we express the spectral shift function arising in a perturbation problem for block operator matrices in terms of the angular operators associated with the corresponding perturbed and unperturbed eigenspaces.

We study the resonances of the operator 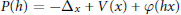$P(h)\,=\,-{{\Delta }_{x}}\,+\,V(x)\,+\,\varphi (hx)$ . Here 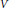$V$ is a periodic potential, 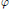$\varphi $ a decreasing perturbation and $h$ a small positive constant. We prove the existence of shape resonances near the edges of the spectral bands of 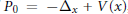${{P}_{0\,}}=\,-{{\Delta }_{x}}\,+\,V(x)$ , and we give its asymptotic expansions in powers of 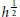${{h}^{\frac{1}{2}}}$ .

The proof of Lemma 3.4 in $\left[ \text{F} \right]$ relies on the incorrect equality ${{\mu }_{j}}(AB)={{\mu }_{j}}(BA)$ for singular values (for a counterexample, see [S, p. 4]). Thus, Theorem 3.1 as stated has not been proven. However, with minor changes, we can obtain a bound for the counting function in terms of the growth of the Fourier transform of $\left| V \right|$ .

The purpose of this note is to provide a simple proof of the sharp polynomial upper bound for the resonance counting function of a Schrödinger operator in odd dimensions. At the same time we generalize the result to the class of superexponentially decreasing potentials.