Given an integer 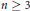 $n\,\ge \,3$ , a metrizable compact topological
$n\,\ge \,3$ , a metrizable compact topological  $n$ -manifold
$n$ -manifold 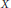 $X$ with boundary, and a finite positive Borel measure
$X$ with boundary, and a finite positive Borel measure  $\mu $ on
$\mu $ on 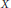 $X$ , we prove that for the typical homeomorphism
$X$ , we prove that for the typical homeomorphism 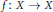 $f\,:\,X\,\to \,X$ , it is true that for
$f\,:\,X\,\to \,X$ , it is true that for  $\mu $ -almost every point
$\mu $ -almost every point  $x$ in
$x$ in 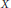 $X$ the limit set
$X$ the limit set 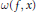 $\omega (f,\,x)$ is a Cantor set of Hausdorff dimension zero, each point of
$\omega (f,\,x)$ is a Cantor set of Hausdorff dimension zero, each point of 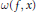 $\omega (f,\,x)$ has a dense orbit in
$\omega (f,\,x)$ has a dense orbit in 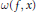 $\omega (f,\,x)$ ,
$\omega (f,\,x)$ , 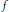 $f$ is non-sensitive at each point of
$f$ is non-sensitive at each point of 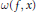 $\omega (f,\,x)$ , and the function
$\omega (f,\,x)$ , and the function 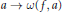 $a\,\to \,\omega (f,\,a)$ is continuous at
$a\,\to \,\omega (f,\,a)$ is continuous at  $x$ .
$x$ .