One-dependent first passage percolation is a spreading process on a graph where the transmission time through each edge depends on the direct surroundings of the edge. In particular, the classical i.i.d. transmission time 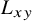$L_{xy}$ is multiplied by 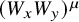$(W_xW_y)^\mu $, a polynomial of the expected degrees 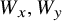$W_x, W_y$ of the endpoints of the edge 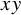$xy$, which we call the penalty function. Beyond the Markov case, we also allow any distribution for 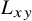$L_{xy}$ with regularly varying distribution near 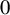$0$. We then run this process on three spatial scale-free random graph models: finite and infinite Geometric Inhomogeneous Random Graphs, including Hyperbolic Random Graphs, and Scale-Free Percolation. In these spatial models, the connection probability between two vertices depends on their spatial distance and on their expected degrees.

We show that as the penalty function, that is, 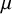$\mu $ increases, the transmission time between two far away vertices sweeps through four universal phases: explosive (with tight transmission times), polylogarithmic, polynomial but strictly sublinear, and linear in the Euclidean distance. The strictly polynomial growth phase is a new phenomenon that so far was extremely rare in spatial graph models. All four growth phases are robust in the model parameters and are not restricted to phase boundaries. Further, the transition points between the phases depend nontrivially on the main model parameters: the tail of the degree distribution, a long-range parameter governing the presence of long edges, and the behaviour of the distribution L near 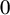$0$. In this paper we develop new methods to prove the upper bounds in all sub-explosive phases. Our companion paper complements these results by providing matching lower bounds in the polynomial and linear regimes.

We study the global well-posedness and uniform boundedness of a two-dimensional reaction–advection–diffusion system with nonlinear advection. This strongly coupled system of nonlinear partial differential equations represents the continuum of a 2D lattice model designed to describe residential burglary, where each location is characterised by a tractability value that varies in both space and time. We show that the model with sublinear advection enhancement is globally well-posed, with a unique solution that is classical and uniformly bounded in time. Our results provide valuable insights into the development of urban crime models with nonlinear advection enhancements, making them suitable for broader applications, including nonlocal or heterogeneous near-repeat victimisation effects.

This corrigendum corrects a result in [1].

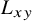
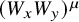
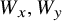
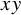
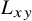
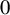
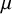
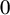
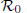We study a susceptible–infected–susceptible reaction–diffusion model with spatially heterogeneous disease transmission and recovery rates. A basic reproduction number is defined for the model. We first prove that there exists a unique endemic equilibrium if 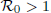. We then consider the global attractivity of the disease-free equilibrium and the endemic equilibrium for two cases. If the disease transmission and recovery rates are constants or the diffusion rate of the susceptible individuals is equal to the diffusion rate of the infected individuals, we show that the disease-free equilibrium is globally attractive if 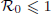, while the endemic equilibrium is globally attractive if .

Entropy maximising spatial interaction models have been widely exploited in a range of disciplines and applications: from trade and migration flows to the spread of riots and the understanding of spatial patterns in archaeological sites of interest. When embedded into a dynamic system and framed in the context of a retail model, the dynamics of centre growth poses an interesting mathematical problem, with bifurcations and phase changes, which may be addressed analytically. In this paper, we present some analysis of the continuous retail model and the corresponding discrete version, which yields insights into the effect of space on the evolving system, and an understanding of why certain retail centres are more successful than others. The slowly developing growths and the fast explosive growths that are of particular concern are explained in detail.

This paper is concerned with the bottom-up hierarchical system and public debate model proposed by Galam (2008), as well as a spatial version of the public debate model. In all three models, there is a population of individuals who are characterized by one of two competing opinions, say opinion −1 and opinion +1. This population is further divided into groups of common size s. In the bottom-up hierarchical system, each group elects a representative candidate, whereas in the other two models, all the members of each group discuss at random times until they reach a consensus. At each election/discussion, the winning opinion is chosen according to Galam's majority rule: the opinion with the majority of representatives wins when there is a strict majority, while one opinion, say opinion −1, is chosen by default in the case of a tie. For the public debate models we also consider the following natural updating rule that we call proportional rule: the winning opinion is chosen at random with a probability equal to the fraction of its supporters in the group. The three models differ in term of their population structure: in the bottom-up hierarchical system, individuals are located on a finite regular tree, in the nonspatial public debate model, they are located on a complete graph, and in the spatial public debate model, they are located on the d-dimensional regular lattice. For the bottom-up hierarchical system and nonspatial public debate model, Galam studied the probability that a given opinion wins under the majority rule and, assuming that individuals' opinions are initially independent, making the initial number of supporters of a given opinion a binomial random variable. The first objective of this paper is to revisit Galam's result, assuming that the initial number of individuals in favor of a given opinion is a fixed deterministic number. Our analysis reveals phase transitions that are sharper under our assumption than under Galam's assumption, particularly with small population size. The second objective is to determine whether both opinions can coexist at equilibrium for the spatial public debate model under the proportional rule, which depends on the spatial dimension.

In this article we study a biased version of the naming game in which players are located on a connected graph and interact through successive conversations in order to select a common name for a given object. Initially, all the players use the same word B except for one bilingual individual who also uses word A. Both words are attributed a fitness, which measures how often players speak depending on the words they use and how often each word is spoken by bilingual individuals. The limiting behavior depends on a single parameter, ϕ, denoting the ratio of the fitness of word A to the fitness of word B. The main objective is to determine whether word A can invade the system and become the new linguistic convention. From the point of view of the mean-field approximation, invasion of word A is successful if and only if ϕ > 3, a result that we also prove for the process on complete graphs relying on the optimal stopping theorem for supermartingales and random walk estimates. In contrast, for the process on the one-dimensional lattice, word A can invade the system whenever ϕ > 1.053, indicating that the probability of invasion and the critical value for ϕ strongly depend on the degree of the graph. The system on regular lattices in higher dimensions is also studied by comparing the process with percolation models.