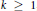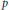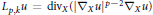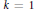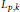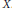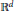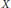Refine search
Actions for selected content:
5 results
A NEW STOPPING PROBLEM AND THE CRITICAL EXERCISE PRICE FOR AMERICAN FRACTIONAL LOOKBACK OPTION IN A SPECIAL MIXED JUMP-DIFFUSION MODEL
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 34 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 21 September 2018, pp. 27-52
-
- Article
- Export citation
The Derivation and Application of Fundamental Solutions for Unsteady Stokes Equations
-
- Journal:
- Journal of Mechanics / Volume 31 / Issue 6 / December 2015
- Published online by Cambridge University Press:
- 18 September 2015, pp. 683-691
- Print publication:
- December 2015
-
- Article
- Export citation
Calculation of Hydrodynamic Forces for Unsteady Stokes Flows by Singularity Integral Equations Based on Fundamental Solutions
-
- Journal:
- Journal of Mechanics / Volume 30 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 08 August 2013, pp. 129-136
- Print publication:
- April 2014
-
- Article
- Export citation
Degenerate p-Laplacian Operators and Hardy Type Inequalities on H-Type Groups
-
- Journal:
- Canadian Journal of Mathematics / Volume 62 / Issue 5 / 01 October 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1116-1130
- Print publication:
- 01 October 2010
-
- Article
-
- You have access
- Export citation
Brownian Motion and Harmonic Analysis on Sierpinski Carpets
-
- Journal:
- Canadian Journal of Mathematics / Volume 51 / Issue 4 / 01 August 1999
- Published online by Cambridge University Press:
- 20 November 2018, pp. 673-744
- Print publication:
- 01 August 1999
-
- Article
-
- You have access
- Export citation