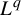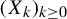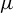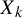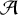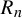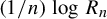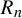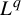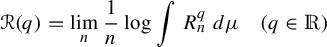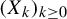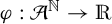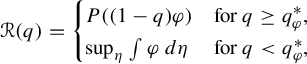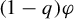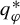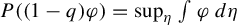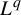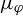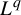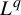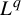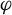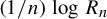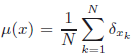Let 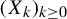 $(X_k)_{k\geq 0}$ be a stationary and ergodic process with joint distribution
$(X_k)_{k\geq 0}$ be a stationary and ergodic process with joint distribution 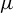 $\mu $, where the random variables
$\mu $, where the random variables 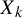 $X_k$ take values in a finite set
$X_k$ take values in a finite set 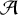 $\mathcal {A}$. Let
$\mathcal {A}$. Let 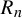 $R_n$ be the first time this process repeats its first n symbols of output. It is well known that
$R_n$ be the first time this process repeats its first n symbols of output. It is well known that 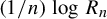 $({1}/{n})\log R_n$ converges almost surely to the entropy of the process. Refined properties of
$({1}/{n})\log R_n$ converges almost surely to the entropy of the process. Refined properties of 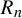 $R_n$ (large deviations, multifractality, etc) are encoded in the return-time
$R_n$ (large deviations, multifractality, etc) are encoded in the return-time 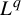 $L^q$-spectrum defined as
$L^q$-spectrum defined as 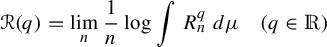
provided the limit exists. We consider the case where 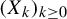 $(X_k)_{k\geq 0}$ is distributed according to the equilibrium state of a potential
$(X_k)_{k\geq 0}$ is distributed according to the equilibrium state of a potential 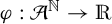 with summable variation, and we prove that
with summable variation, and we prove that 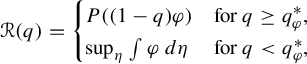
where  $P((1-q)\varphi )$ is the topological pressure of
$P((1-q)\varphi )$ is the topological pressure of 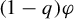 $(1-q)\varphi $, the supremum is taken over all shift-invariant measures, and
$(1-q)\varphi $, the supremum is taken over all shift-invariant measures, and 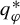 $q_\varphi ^*$ is the unique solution of
$q_\varphi ^*$ is the unique solution of 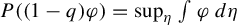 $P((1-q)\varphi ) =\sup _\eta \int \varphi \,d\eta $. Unexpectedly, this spectrum does not coincide with the
$P((1-q)\varphi ) =\sup _\eta \int \varphi \,d\eta $. Unexpectedly, this spectrum does not coincide with the 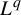 $L^q$-spectrum of
$L^q$-spectrum of 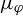 $\mu _\varphi $, which is
$\mu _\varphi $, which is  $P((1-q)\varphi )$, and it does not coincide with the waiting-time
$P((1-q)\varphi )$, and it does not coincide with the waiting-time 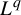 $L^q$-spectrum in general. In fact, the return-time
$L^q$-spectrum in general. In fact, the return-time 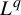 $L^q$-spectrum coincides with the waiting-time
$L^q$-spectrum coincides with the waiting-time 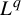 $L^q$-spectrum if and only if the equilibrium state of
$L^q$-spectrum if and only if the equilibrium state of 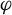 $\varphi $ is the measure of maximal entropy. As a by-product, we also improve the large deviation asymptotics of
$\varphi $ is the measure of maximal entropy. As a by-product, we also improve the large deviation asymptotics of 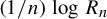 $({1}/{n})\log R_n$.
$({1}/{n})\log R_n$.
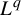 $L^q$-spectrum for equilibrium states with potentials of summable variation
$L^q$-spectrum for equilibrium states with potentials of summable variation